适用年级:{{getGradeNameByProperty('初三|中考模拟|浙江|2014年')}} 试卷类型:{{getTestPaperTypeName('初三|中考模拟|浙江|2014年')}} 使用省份:{{getAreaName('初三|中考模拟|浙江|2014年')}}
试卷年份:{{getYear('初三|中考模拟|浙江|2014年')}}上传日期:2014-08-11题数:23
提示:单击题文可显示答案与解析。
题号:634660
题型:选择题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】以下说法:
①关于x的方程
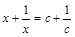
的解是x=c(c≠0);
②方程组

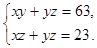
正整数的解有2组;
③已知关于x,y的方程组
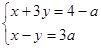
,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;其中正确的有( )
题号:634661
题型:选择题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】在平面直角坐标系中,设点P到原点O的距离为
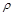
,OP与x轴正方向的夹角为
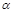
,则用[
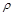
,
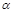
]表示点P的极坐标;显然,点P的极坐标与它的坐标存在一一对应的关系.例如,点P的坐标(1,1),则极坐标为[
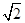
,45°].若点Q的极坐标为[4,60°],则点Q的坐标为( )
题号:634662
题型:选择题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】小兰画了一个函数
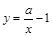
的图象如图,那么关于x的分式方程
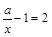
的解是( )
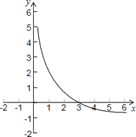
| A.x=1 | B.x="2" | C.x="3" | D.x="4" |
题号:634663
题型:选择题
难易度:较易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
题号:634664
题型:选择题
难易度:较易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是()
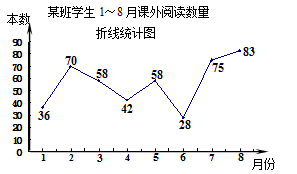
| A.极差是47 |
| B.众数是42 |
| C.中位数是58 |
| D.每月阅读数量超过40的有4个月 |
题号:634665
题型:选择题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
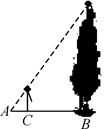
【题文】如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
题号:634666
题型:选择题
难易度:较易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】如果
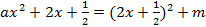
,则
a,
m的值分别是( )
| A.2,0 | B.4,0 | C.2, | D.4, |
题号:634667
题型:选择题
难易度:容易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
题号:3937957
题型:选择题
难易度:较易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
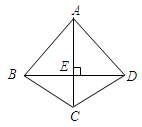
【题文】如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
| A.AB=AD | B.AC平分∠BCD | C.AB=BD | D.△BEC≌△DEC |
题号:3937958
题型:选择题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
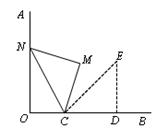
【题文】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则
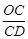
的值为( )
题号:634654
题型:填空题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
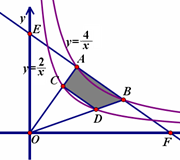
【题文】已知,如图双曲线
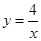
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线
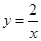
(x>0)交于点C,点D,则:
(1)AB与CD的位置关系是__________;
(2)四边形ABDC的面积为__________.
题号:634655
题型:填空题
难易度:较易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
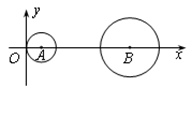
【题文】如图,已知点A(1,0)、B(7,0),⊙A、⊙B的半径分别为1和2,当⊙A与⊙B相切时,应将⊙A沿
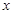
轴向右平移__________个单位.
题号:634656
题型:填空题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
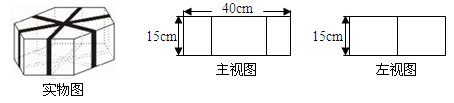
【题文】如图,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为__________cm.(不计接缝,结果保留准确值)
题号:634657
题型:填空题
难易度:较易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
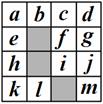
【题文】如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形,使黑色部分成为轴对称图形,这样的白色小方格有:__________(填字母).
题号:634658
题型:填空题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】数据
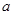
,4,2,5,3的平均数为
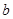
,且
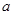
和
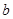
是方程
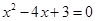
的两个根,则这组数据的标准差是________.
题号:634659
题型:填空题
难易度:较易
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】已知无理数1+2
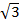
,若
a<1+2
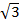
<
b,其中
a、
b为两个连续的整数,则
ab的值为__________.
题号:634647
题型:解答题
难易度:困难
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】已知抛物线y=3ax
2+2bx+c
(1)若a=b=1,c=-1求该抛物线与x轴的交点坐标;
(2)若a=
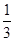
,c=2+b且抛物线在
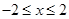
区间上的最小值是-3,求b的值;
(3)若a+b+c=1,是否存在实数x,使得相应的y的值为1,请说明理由.
题号:634648
题型:解答题
难易度:困难
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
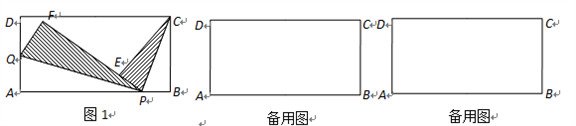
【题文】如图1,在矩形
ABCD中,
AB=4,
AD=2,点
P是边
AB上的一个动点(不与点
A、点
B重合),点
Q在边
AD上,将△
CBP和△
QAP分别沿
PC、
PQ折叠,使
B点与
E点重合,
A点与
F点重合,且
P、
E、
F三点共线.
(1)若点
E平分线段
PF,则此时
AQ的长为多少?
(2)若线段
CE与线段
QF所在的平行直线之间的距离为2,则此时
AP的长为多少?
(3)在“线段
CE”、“线段
QF”、“点
A”这三者中,是否存在两个在同一条直线上的情况?若存在,求出此时
AP的长;若不存在,请说明理由.
题号:634649
题型:解答题
难易度:较难
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
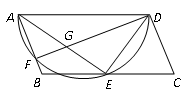
【题文】如图,在平行四边形
ABCD中,
E为
BC边上的一点,且
AE与
DE分别平分
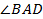
和
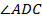
(1)求证:
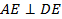
;
(2)设以
AD为直径的半圆交
AB于
F,连结
DF交
AE于
G,已知
CD=5,
AE=8.
①求
BC的长;
②求
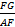
值.
题号:634650
题型:解答题
难易度:较难
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
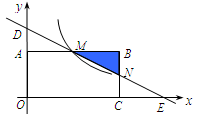
【题文】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数
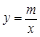
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
题号:634652
题型:解答题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】先化简,再求代数式的值:
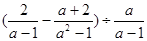
,其中sin
230°<
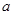
<tan
260°,请你取一个合适的整数作为
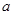
的值代入求值.
题号:634653
题型:解答题
难易度:一般
日期:2014-08-11
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】请用直尺和圆规在所给的两个矩形中各作一个不为正方形的菱形,且菱形的四个顶点都在矩形的边上,面积相同的图形视为同一种. (保留作图痕迹).


题号:3902952
题型:解答题
难易度:一般
日期:2017-07-26
来源:2014届浙江省杭州市拱墅区中考二模考试数学试卷(带解析)
【题文】在一个不透明的盒子里,装有四个分别标有数字
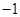
,
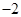
,
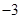
,
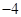
的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数
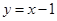
的图象上的概率;
(3)求小强、小华各取一次小球所确定的数x、y满足
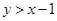
的概率.
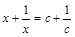 的解是x=c(c≠0);
的解是x=c(c≠0);
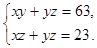 正整数的解有2组;
正整数的解有2组;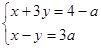 ,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;其中正确的有( )
,其中﹣3≤a≤1,当a=1时,方程组的解也是方程x+y=4﹣a的解;其中正确的有( )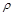 ,OP与x轴正方向的夹角为
,OP与x轴正方向的夹角为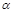 ,则用[
,则用[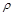 ,
,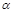 ]表示点P的极坐标;显然,点P的极坐标与它的坐标存在一一对应的关系.例如,点P的坐标(1,1),则极坐标为[
]表示点P的极坐标;显然,点P的极坐标与它的坐标存在一一对应的关系.例如,点P的坐标(1,1),则极坐标为[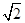 ,45°].若点Q的极坐标为[4,60°],则点Q的坐标为( )
,45°].若点Q的极坐标为[4,60°],则点Q的坐标为( )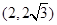
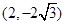
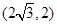
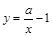 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程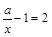 的解是( )
的解是( )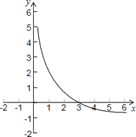
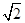 r
r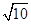 r
r

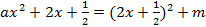 ,则a,m的值分别是( )
,则a,m的值分别是( )

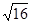 的值等于( )
的值等于( )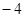
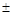 2
2
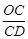 的值为( )
的值为( )
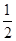
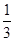
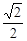
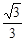
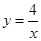 (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线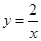 (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
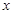 轴向右平移__________个单位.
轴向右平移__________个单位.


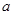 ,4,2,5,3的平均数为
,4,2,5,3的平均数为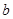 ,且
,且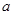 和
和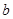 是方程
是方程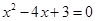 的两个根,则这组数据的标准差是________.
的两个根,则这组数据的标准差是________.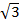 ,若a<1+2
,若a<1+2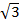 <b,其中a、b为两个连续的整数,则ab的值为__________.
<b,其中a、b为两个连续的整数,则ab的值为__________.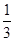 ,c=2+b且抛物线在
,c=2+b且抛物线在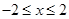 区间上的最小值是-3,求b的值;
区间上的最小值是-3,求b的值;
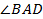 和
和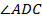
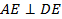 ;
;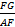 值.
值.
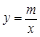 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
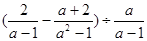 ,其中sin230°<
,其中sin230°<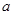 <tan260°,请你取一个合适的整数作为
<tan260°,请你取一个合适的整数作为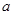 的值代入求值.
的值代入求值.

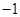 ,
,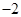 ,
,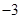 ,
,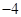 的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.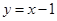 的图象上的概率;
的图象上的概率;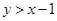 的概率.
的概率.