适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-17题数:20
提示:单击题文可显示答案与解析。
题号:934216
题型:填空题
难易度:较易
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知F1、F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=________.
题号:934217
题型:填空题
难易度:一般
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】F
1,F
2是椭圆
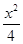
+y
2=1的左右焦点,点P在椭圆上运动.则
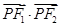
的最大值是________.
题号:934218
题型:填空题
难易度:较易
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知F
1、F
2是椭圆C:
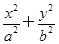
=1(a>b>0)的两个焦点,P为椭圆C上一点,且
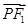
⊥
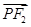
.若△PF
1F
2的面积为9,则b=________.
题号:934219
题型:填空题
难易度:较易
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为
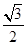
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______________.
题号:4186711
题型:填空题
难易度:一般
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知F是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交C于点D,且
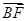
=2
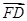
,则C的离心率为________.
题号:934161
题型:解答题
难易度:一般
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
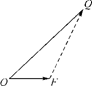
【题文】如图,已知△OFQ的面积为S,且
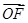
·
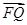
=1.设|
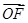
|=c(c≥2),S=
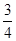
c.若以O为中心,F为一个焦点的椭圆经过点Q,当|
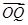
|取最小值时,求椭圆的方程.
题号:934163
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知椭圆C:
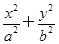
=1(a>b>0)经过点M(-2,-1),离心率为
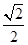
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
(1)求椭圆C的方程;
(2)试判断直线PQ的斜率是否为定值,证明你的结论.
题号:934164
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知椭圆
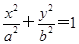
=1(a>b>0),点P
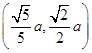
在椭圆上.
(1)求椭圆的离心率;
(2)设A为椭圆的左顶点,O为坐标原点.若点Q在椭圆上且满足AQ=AO,求直线OQ的斜率的值.
题号:934165
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
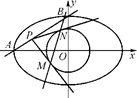
【题文】如图,正方形ABCD内接于椭圆
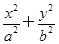
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
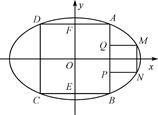
(1)若正方形ABCD的边长为4,且与y轴交于E、F两点,正方形MNPQ的边长为2.
①求证:直线AM与△ABE的外接圆相切;
②求椭圆的标准方程;
(2)设椭圆的离心率为e,直线AM的斜率为k,求证:2e
2-k是定值.
题号:934166
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】如图,在平面直角坐标系xOy中,已知F
1,F
2分别是椭圆E:
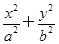
=1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且
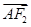
+5
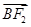
=0.
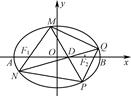
(1)求椭圆E的离心率; (2)已知点D(1,0)为线段OF
2的中点,M为椭圆E上的动点(异于点A、B),连结MF
1并延长交椭圆E于点N,连结MD、ND并分别延长交椭圆E于点P、Q,连结PQ,设直线MN、PQ的斜率存在且分别为k
1、k
2,试问是否存在常数λ,使得k
1+λk
2=0恒成立?若存在,求出λ的值;若不存在,说明理由.
题号:934167
题型:解答题
难易度:困难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】如图,已知椭圆
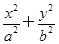
=1(a>b>0)的离心率为
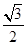
,且过点A(0,1).
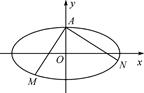
(1)求椭圆的方程;
(2)过点A作两条互相垂直的直线分别交椭圆于点M、N,求证:直线MN恒过定点P
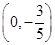
.
题号:934168
题型:解答题
难易度:一般
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知直线l经过点(1,0)且一个方向向量
d=(1,1).椭圆C:
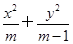
=1(m>1)的左焦点为F
1.若直线l与椭圆C交于A,B两点,满足
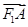
·
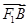
=0,求实数m的值.
题号:934169
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知曲线C:(5-m)x2+(m-2)y2=8(m∈R).
(1)若曲线C是焦点在x轴上的椭圆,求m的取值范围;
(2)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M,N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.
题号:934170
题型:解答题
难易度:一般
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知椭圆C:
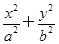
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x
2+y
2=
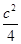
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(1)若椭圆C经过两点
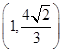
、
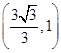
,求椭圆C的方程;
(2)当c为定值时,求证:直线MN经过一定点E,并求
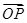
·
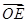
的值(O是坐标原点);
(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围..
题号:934171
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知椭圆的中心为坐标原点O,椭圆短半轴长为1,动点M(2,t)(t>0)在直线x=
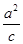
(a为长半轴,c为半焦距)上.
(1)求椭圆的标准方程;
(2)求以OM为直径且被直线3x-4y-5=0截得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值.
题号:934212
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】如图,在平面直角坐标系xOy中,椭圆C:
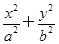
=1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为
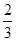
,点M的横坐标为
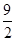
.
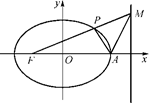
(1)求椭圆C的标准方程;
(2)设直线PA的斜率为k
1,直线MA的斜率为k
2,求k
1·k
2的取值范围.
题号:934213
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】设A、B分别为椭圆
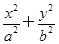
=1(a>b>0)的左、右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线.
(1)求椭圆的方程;
(2)设P为椭圆右准线上不同于点(4,0)的任意一点,若直线BP与椭圆相交于两点B、N,求证:∠NAP为锐角.
题号:934214
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知椭圆的右焦点F
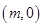
,左、右准线分别为l
1:x=-m-1,l
2:x=m+1,且l
1、l
2分别与直线y=x相交于A、B两点.
(1)若离心率为
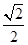
,求椭圆的方程;
(2)当
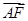
·
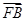
<7时,求椭圆离心率的取值范围.
题号:934215
题型:解答题
难易度:一般
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】如图,F
1、F
2是椭圆
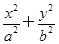
=1(a>b>0)的左、右焦点,点M在x轴上,且
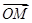
=
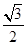
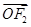
,过点F
2的直线与椭圆交于A、B两点,且AM⊥x轴,
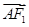
·
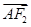
=0.
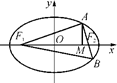
(1)求椭圆的离心率;
(2)若△ABF
1的周长为
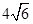
,求椭圆的方程.
题号:4186712
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届高考数学总复习考点引领+技巧点拨第九章第7课时练习卷(带解析)
【题文】已知椭圆
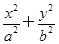
=1(a>b>0)的离心率为
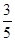
,且过点P
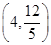
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
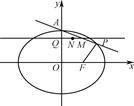
(1)求椭圆方程;
(2)若圆N与x轴相切,求圆N的方程;
(3)设点R为圆N上的动点,点R到直线PF的最大距离为d,求d的取值范围.
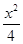 +y2=1的左右焦点,点P在椭圆上运动.则
+y2=1的左右焦点,点P在椭圆上运动.则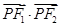 的最大值是________.
的最大值是________.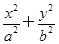 =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且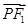 ⊥
⊥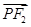 .若△PF1F2的面积为9,则b=________.
.若△PF1F2的面积为9,则b=________.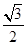 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______________.
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______________.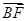 =2
=2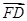 ,则C的离心率为________.
,则C的离心率为________.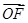 ·
·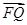 =1.设|
=1.设|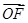 |=c(c≥2),S=
|=c(c≥2),S=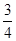 c.若以O为中心,F为一个焦点的椭圆经过点Q,当|
c.若以O为中心,F为一个焦点的椭圆经过点Q,当|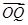 |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.
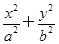 =1(a>b>0)经过点M(-2,-1),离心率为
=1(a>b>0)经过点M(-2,-1),离心率为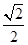 .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.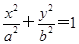 =1(a>b>0),点P
=1(a>b>0),点P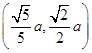 在椭圆上.
在椭圆上.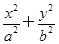 =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
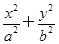 =1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且
=1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且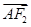 +5
+5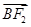 =0.
=0.
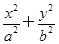 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为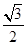 ,且过点A(0,1).
,且过点A(0,1).
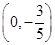 .
.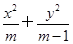 =1(m>1)的左焦点为F1.若直线l与椭圆C交于A,B两点,满足
=1(m>1)的左焦点为F1.若直线l与椭圆C交于A,B两点,满足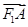 ·
·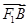 =0,求实数m的值.
=0,求实数m的值.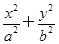 =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=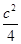 (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
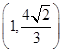 、
、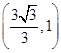 ,求椭圆C的方程;
,求椭圆C的方程;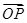 ·
·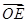 的值(O是坐标原点);
的值(O是坐标原点);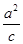 (a为长半轴,c为半焦距)上.
(a为长半轴,c为半焦距)上.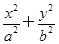 =1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为
=1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为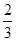 ,点M的横坐标为
,点M的横坐标为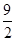 .
.
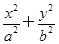 =1(a>b>0)的左、右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线.
=1(a>b>0)的左、右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线.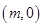 ,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点.
,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点.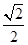 ,求椭圆的方程;
,求椭圆的方程;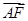 ·
·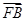 <7时,求椭圆离心率的取值范围.
<7时,求椭圆离心率的取值范围.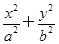 =1(a>b>0)的左、右焦点,点M在x轴上,且
=1(a>b>0)的左、右焦点,点M在x轴上,且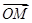 =
=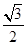
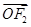 ,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,
,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,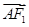 ·
·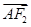 =0.
=0.
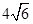 ,求椭圆的方程.
,求椭圆的方程.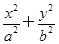 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为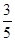 ,且过点P
,且过点P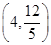 ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.