适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-14题数:20
提示:单击题文可显示答案与解析。
题号:935479
题型:填空题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】若平面α的一个法向量为n=(4,1,1),直线l的一个方向向量为a=(-2,-3,3),则l与α所成角的正弦值为________.
题号:935480
题型:填空题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】设A
1、A
2、A
3、A
4、A
5是空间中给定的5个不同的点,则使
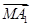
+
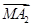
+
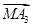
+
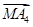
+
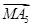
=0成立的点M的个数为________.
题号:935485
题型:填空题
难易度:较易
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
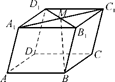
【题文】如图,在平行六面体ABCDA
1B
1C
1D
1中,M为A
1C
1与B
1D
1的交点.若
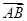
=
a,
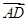
=
b,
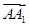
=
c,则
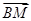
=________.
题号:935486
题型:填空题
难易度:较易
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
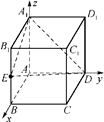
【题文】在正方体ABCDA
1B
1C
1D
1中,点E为BB
1的中点,则平面A
1ED与平面ABCD所成的锐二面角的余弦值为________.
题号:935487
题型:填空题
难易度:较易
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a、b、c三个向量共面,则实数λ等于________.
题号:935488
题型:填空题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】已知l∥α,且l的方向向量为(2,m,1),平面α的法向量为
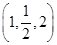
,则m=________.
题号:935489
题型:填空题
难易度:较易
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
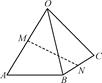
【题文】已知空间四边形OABC,点M、N分别是OA、BC的中点,且
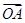
=
a,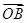
=
b,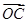
=
c,用
a,
b,
c表示向量
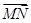
=________.
题号:935490
题型:填空题
难易度:较易
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】若向量
a=(1,λ,2),
b=(2,-1,2)且
a与
b的夹角的余弦值为
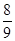
,则λ=________.
题号:935472
题型:解答题
难易度:较难
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
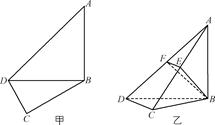
(1)求证:DC⊥平面ABC;
(2)求BF与平面ABC所成角的正弦值;
(3)求二面角B-EF-A的余弦值.
题号:935473
题型:解答题
难易度:较难
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如图,在三棱柱ABCA
1B
1C
1中,A
1B⊥平面ABC,AB⊥AC,且AB=AC=A
1B=2.
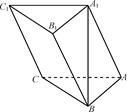
(1)求棱AA
1与BC所成的角的大小;
(2)在棱B
1C
1上确定一点P,使二面角P-AB-A
1的平面角的余弦值为
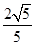
.
题号:935474
题型:解答题
难易度:较难
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】三棱柱ABC-A
1B
1C
1在如图所示的空间直角坐标系中,已知AB=2,AC=4,A
1A=3.D是BC的中点.
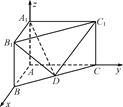
(1)求直线DB
1与平面A
1C
1D所成角的正弦值;
(2)求二面角B
1-A
1D-C
1的正弦值.
题号:935475
题型:解答题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
(1)求二面角D1-AE-C的大小;
(2)求证:直线BF∥平面AD1E.
题号:935476
题型:解答题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】在三棱锥SABC中,底面是边长为2
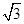
的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.
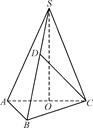
(1)若D为侧棱SB上一点,当
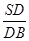
为何值时,CD⊥AB;
(2)求二面角S-BC-A的余弦值大小.
题号:935477
题型:解答题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如图所示,四棱锥PABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=
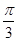
,F为PC的中点,AF⊥PB.
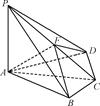
(1)求PA的长;
(2)求二面角B-AF-D的正弦值.
题号:935478
题型:解答题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如图所示,直三棱柱ABCA
1B
1C
1中,D、E分别是AB、BB
1的中点,AA
1=AC=CB=
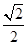
AB.
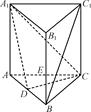
(1)证明:BC
1∥平面A
1CD;
(2)求二面角DA
1CE的正弦值..
题号:935481
题型:解答题
难易度:较难
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如图,圆锥的高PO=4,底面半径OB=2,D为PO的中点,E为母线PB的中点,F为底面圆周上一点,满足EF⊥DE.
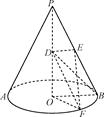
(1)求异面直线EF与BD所成角的余弦值;
(2)求二面角OOFE的正弦值.
题号:935482
题型:解答题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如右图,在棱长为a的正方体ABCDA
1B
1C
1D
1中,G为△BC
1D的重心,
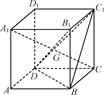
(1)试证:A
1、G、C三点共线;
(2)试证:A
1C⊥平面BC
1D;
题号:935483
题型:解答题
难易度:较难
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
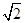
,AF=1,M是线段EF的中点.
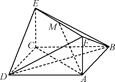
求证:(1)AM∥平面BDE;
(2)AM⊥平面BDF.
题号:935484
题型:解答题
难易度:一般
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4).设
a=
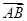
,
b=
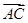
.
(1)求
a和
b的夹角θ;
(2)若向量k
a+
b与k
a-2
b互相垂直,求k的值.
题号:4186783
题型:解答题
难易度:较难
日期:2014-04-14
来源:2014届高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(带解析)
【题文】如图所示,在直三棱柱A
1B
1C
1-ABC中,AB⊥AC,AB=AC=2,A
1A=4,点D是BC的中点.
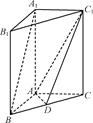
(1)求异面直线A
1B与C
1D所成角的余弦值;
(2)求平面ADC
1与平面ABA
1所成二面角的正弦值.
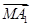 +
+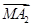 +
+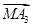 +
+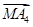 +
+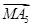 =0成立的点M的个数为________.
=0成立的点M的个数为________.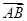 =a,
=a,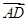 =b,
=b,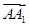 =c,则
=c,则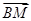 =________.
=________.

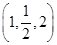 ,则m=________.
,则m=________.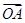 =a,
=a,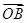 =b,
=b,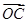 =c,用a,b,c表示向量
=c,用a,b,c表示向量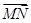 =________.
=________.
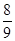 ,则λ=________.
,则λ=________.

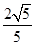 .
.
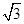 的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.
的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.
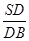 为何值时,CD⊥AB;
为何值时,CD⊥AB;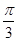 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
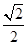 AB.
AB.


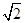 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
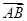 ,b=
,b=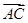 .
.