适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948551
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
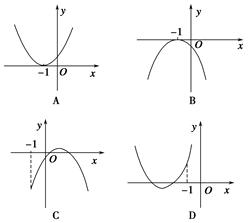
【题文】设函数
f(
x)=
ax2+
bx+
c(
a,
b,
c∈R),若
x=-1为函数
f(
x)e
x的一个极值点,则下列图象不可能为
y=
f(
x)的图象是( ).
题号:948572
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】设函数f(x)=xe
x,则( )
| A.x=1为f(x)的极大值点 | B.x=1为f(x)的极小值点 |
| C.x=-1为f(x)的极大值点 | D.x=-1为f(x)的极小值点 |
题号:948573
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】若
S1=
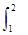 x2
x2d
x,
S2=
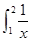
d
x,
S3=
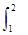
e
xd
x,则
S1,
S2,
S3的大小关系为( ).
| A.S1<S2<S3 | B.S2<S1<S3 |
| C.S2<S3<S1 | D.S3<S2<S1 |
题号:948574
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】函数
y=
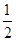 x2
x2-ln
x的单调减区间是 ( ).
| A.(-1,1] | B.(0,1] | C.[1,+∞) | D.(0,+∞) |
题号:4880957
题型:选择题
难易度:一般
日期:2017-09-02
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】已知函数
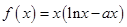
有两个极值点,则实数
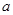
的取值范围是( )
题号:948548
题型:填空题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】设直线x=t,与函数f(x)=x2,g(x)=ln x的图象分别交于点M,N,则当|MN|达到最小时t的值为________.
题号:948549
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】已知函数f(x)=

mx
2+ln x-2x在定义域内是增函数,则实数m的取值范围为________.
题号:4187756
题型:填空题
难易度:一般
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】若曲线y=xα+1(α∈R)在点(1,2)处的切线经过坐标原点,则α=________.
题号:948545
题型:解答题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】已知函数
f(
x)=
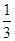 x3
x3+
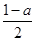 x2
x2-
ax-
a,
x∈R,其中
a>0.
(1)求函数
f(
x)的单调区间;
(2)若函数
f(
x)在区间(-2,0)内恰有两个零点,求
a的取值范围.
题号:948546
题型:解答题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】设函数f(x)=x+ax2+bln x,曲线y=f(x)在点P(1,0)处的切线斜率为2.
(1)求a,b的值;
(2)证明:f(x)≤2x-2.
题号:948547
题型:解答题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(带解析)
【题文】已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值.

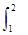 x2dx,S2=
x2dx,S2=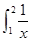 dx,S3=
dx,S3=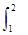 exdx,则S1,S2,S3的大小关系为( ).
exdx,则S1,S2,S3的大小关系为( ).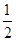 x2-ln x的单调减区间是 ( ).
x2-ln x的单调减区间是 ( ).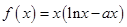 有两个极值点,则实数
有两个极值点,则实数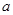 的取值范围是( )
的取值范围是( )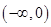
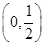
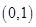
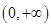
 mx2+ln x-2x在定义域内是增函数,则实数m的取值范围为________.
mx2+ln x-2x在定义域内是增函数,则实数m的取值范围为________.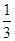 x3+
x3+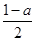 x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.