适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-11题数:15
提示:单击题文可显示答案与解析。
题号:936679
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则a+b+c=________.
题号:936680
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】某科研单位欲拿出一定的经费奖励科研人员,第1名得全部资金的一半多一万元,第2名得剩下的一半多一万元,以名次类推都得到剩下的一半多一万元,到第10名恰好资金分完,则此科研单位共拿出________万元资金进行奖励.
题号:936684
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】已知公差不为0的等差数列{a
n}满足a
1,a
3,a
9成等比数列,S
n为数列{a
n}的前n项和,则
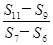
=________.
题号:4186849
题型:填空题
难易度:较易
日期:2014-04-13
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵树是前一天的2倍,则需要的最少天数n(n∈N*)为________.
题号:936677
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】甲、乙两大超市同时开业,第一年的全年销售额均为a万元,由于经营方式不同,甲超市前n年的总销售额为
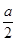
(n
2-n+2)万元,乙超市第n年的销售额比前一年销售额多
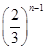
a万元.
(1)设甲、乙两超市第n年的销售额分别为a
n、b
n,求a
n、b
n的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?
题号:936678
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】我国是一个人口大国,随着时间推移,老龄化现象越来越严重,为缓解社会和家庭压力,决定采用养老储备金制度.公民在就业的第一年交纳养老储备金,数目为a1,以后每年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的储备金数目a1,a2,…,an是一个公差为d的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定利率为r(r>0),那么,在第n年末,第一年所交纳的储备金就变为a1(1+r)n-1,第二年所交纳的储备金就变为a2(1+r)n-2,…,以Tn表示到第n年所累计的储备金总额.
(1)写出Tn与Tn-1(n≥2)的递推关系式;
(2)求证:Tn=An+Bn,其中{An}是一个等比数列,{Bn}是一个等差数列.
题号:936681
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】已知数列{a
n}前n项和为S
n,且a
2a
n=S
2+S
n对一切正整数都成立.
(1)求a
1,a
2的值;
(2)设a
1>0,数列
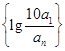
前n项和为T
n,当n为何值时,T
n最大?并求出最大值.
题号:936682
题型:解答题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
题号:936683
题型:解答题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】已知等差数列{an}的公差d=1,前n项和为Sn.
(1)若1,a1,a3成等比数列,求a1;
(2)若S5>a1a9,求a1的取值范围.
题号:936685
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】已知数列{an}是首项为1,公差为d的等差数列,数列{bn}是首项为1,公比为q(q>1)的等比数列.
(1)若a5=b5,q=3,求数列{an·bn}的前n项和;
(2)若存在正整数k(k≥2),使得ak=bk.试比较an与bn的大小,并说明理由..
题号:936686
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】已知等差数列{a
n}满足:a
n+1>a
n(n∈N
*),a
1=1,该数列的前三项分别加上1,1,3后顺次成为等比数列{b
n}的前三项.
(1)分别求数列{a
n}、{b
n}的通项公式;
(2)设T
n=
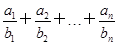
(n∈N
*),若T
n+
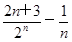
<c(c∈Z)恒成立,求c的最小值.
题号:936687
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】已知各项均为正数的等比数列{a
n}的公比为q,且0<q<
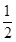
.
(1)在数列{a
n}中是否存在三项,使其成等差数列?说明理由;
(2)若a
1=1,且对任意正整数k,a
k-(a
k+1+a
k+2)仍是该数列中的某一项.
(ⅰ)求公比q;
(ⅱ)若b
n=-loga
n+1(
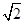
+1),S
n=b
1+b
2+…+b
n,T
r=S
1+S
2+…+S
n,试用S
2011表示T
2011.
题号:936688
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
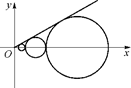
【题文】设C
1、C
2、…、C
n、…是坐标平面上的一列圆,它们的圆心都在轴的正半轴上,且都与直线y=
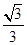
x相切,对每一个正整数n,圆C
n都与圆C
n+1相互外切,以r
n表示C
n的半径,已知{r
n}为递增数列.
(1)证明:{r
n}为等比数列;
(2)设r
1=1,求数列
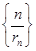
的前n项和.
题号:936689
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】水土流失是我国西部大开发中最突出的问题,全国9100万亩坡度为25°以上的坡耕地需退耕还林,其中西部占70%,2002年国家确定在西部地区退耕还林面积为515万亩,以后每年退耕土地面积递增12%.
(1)试问,从2002年起到哪一年西部地区基本上解决退耕还林问题?
(2)为支持退耕还林工作,国家财政补助农民每亩300斤粮食,每斤粮食按0.7元计算,并且每亩退耕地每年补助20元,试问到西部地区基本解决退耕还林问题时,国家财政共需支付约多少亿元?
题号:936690
题型:解答题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(带解析)
【题文】某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备x年的年平均污水处理费用y(万元);
(2)为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
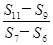 =________.
=________.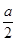 (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多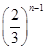 a万元.
a万元.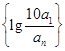 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.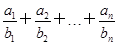 (n∈N*),若Tn+
(n∈N*),若Tn+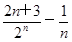 <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.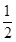 .
.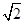 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.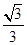 x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
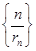 的前n项和.
的前n项和.