适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-11题数:20
提示:单击题文可显示答案与解析。
题号:701888
题型:填空题
难易度:较易
日期:2016-10-31
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知等比数列{an}是递增数列,Sn是{an}的前n项和,若a1,a3是方程x2-5x+4=0的两个根,则S6=________.
题号:936753
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】若数列{an}满足lgan+1=1+lgan,a1+a2+a3=10,则lg(a4+a5+a6)=________.
题号:936754
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】等比数列{an}的前n项和为Sn,已知S3=a2+10a1,a5=9,则a1=________.
题号:936755
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】若数列{a
n}的前n项和为S
n=
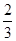
a
n+
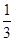
,则数列{a
n}的通项公式是a
n=________.
题号:936756
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知数列{a
n}满足3a
n+1+a
n=0,a
2=-
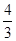
,则{a
n}的前10项和为________.
题号:936758
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知{a
n}是等比数列,a
2=2,a
5=
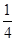
,则a
1a
2+a
2a
3+…+a
na
n+1(n∈N
*)的取值范围是________.
题号:936763
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】等比数列{an}中,S3=7,S6=63,则an=________.
题号:936764
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知两个数k+9和6-k的等比中项是2k,则k=________.
题号:936765
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】等比数列{an}中,a1>0,a2a4+2a3a5+a4a6=36,则a3+a5=________.
题号:936766
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】{an}为等比数列,a2=6,a5=162,则{an}的通项公式an=________.
题号:936767
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】设Sn是等比数列{an}的前n项和,若a1=1,a6=32,则S3=________.
题号:3428475
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{a
n},{f(a
n)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(-∞,0)∪(0,+∞)上的如下函数:
①f(x)=x
2;②f(x)=2
x;③f(x)=
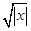
;④f(x)=ln(x).
其中是“保等比数列函数”的是__________.(填序号)
题号:936729
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1)证明:{bn}从第2项起是以2为公比的等比数列;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3)当a>0时,求数列{an}的最小项.
题号:936731
题型:解答题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知数列{an}的前n项和为Sn,a1=1,Sn+1=4an+1,设bn=an+1-2an.证明:数列{bn}是等比数列.
题号:936752
题型:解答题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】等比数列{an}的前n项和为Sn,已知a1+an=66,a2an-1=128,Sn=126,求n和公比q的值.
题号:936757
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知数列{a
n}的前n项和S
n=2n
2+2n,数列{b
n}的前n项和T
n=2-b
n.
(1)求数列{a
n}与{b
n}的通项公式;
(2)设c
n=
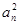
·b
n,证明:当且仅当n≥3时,c
n+1<c
n..
题号:936759
题型:解答题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知等比数列{a
n}中,a
2=32,a
8=
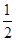
,a
n+1<a
n.
(1)求数列{a
n}的通项公式;
(2)设T
n=log
2a
1+log
2a
2+…+log
2a
n,求T
n的最大值及相应的n值.
题号:936760
题型:解答题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1)求证:数列{an-n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)求证:不等式Sn+1≤4Sn对任意n∈N*皆成立.
题号:936761
题型:解答题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】已知数列{an}的前n项和为Sn,3Sn=an-1(n∈N).
(1)求a1,a2;
(2)求证:数列{an}是等比数列;
(3)求an和Sn.
题号:936762
题型:解答题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(带解析)
【题文】等比数列{an}的前n项和为Sn,已知S1,S3,S2成等差数列.
(1)求{an}的公比q;
(2)若a1-a3=3,求Sn.
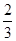 an+
an+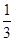 ,则数列{an}的通项公式是an=________.
,则数列{an}的通项公式是an=________.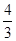 ,则{an}的前10项和为________.
,则{an}的前10项和为________.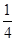 ,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.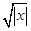 ;④f(x)=ln(x).
;④f(x)=ln(x).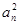 ·bn,证明:当且仅当n≥3时,cn+1<cn..
·bn,证明:当且仅当n≥3时,cn+1<cn..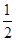 ,an+1<an.
,an+1<an.