适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-11题数:18
提示:单击题文可显示答案与解析。
题号:936642
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】在数列{an}中,已知a1=2,a2=3,当n≥2时,an+1是an·an-1的个位数,则a2010=________.
题号:936643
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】在正项等比数列{a
n}中,a
5=
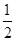
,a
6+a
7=3,则满足a
1+a
2+…+a
n>a
1a
2…a
n的最大正整数n的值为________.
题号:936644
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】等差数列{an}的前n项和为Sn,已知S10=0,S15=25,则nSn的最小值为________.
题号:936645
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】若等差数列的前6项和为23,前9项和为57,则数列的前n项和Sn=________.
题号:936646
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和.若a1,a2,a5成等比数列,则S8=________.
题号:936673
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】已知数列{an},{bn}满足a1=1,且an、an+1是函数f(x)=x2-bnx+2n的两个零点,则b10=________.
题号:936674
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】设1=a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等
比数列,a2,a4,a6成公差为1的等差数列,则q的最小值是________.
题号:936675
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】已知等差数列{a
n}的前n项和为S
n,若
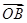
=a
100·
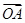
+a
101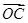
,且A、B、C三点共线(该直线不过点O),则S
200=________.
题号:936676
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量S
n(万件)近似地满足关系式S
n=
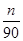
(21n-n
2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
题号:936639
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】已知数列{a
n},其前n项和为S
n.
(1)若对任意的n∈N,a
2n-1,a
2n+1,a
2n组成公差为4的等差数列,且a
1=1,
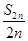
=2013,求n的值;
(2)若数列
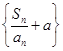
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{a
n}为等比数列的充要条件为q=1+
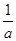
.
题号:936640
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】设不等式组
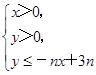
所表示的平面区域为D
n,记D
n内的整点个数为a
n(n∈N
*)(整点即横坐标和纵坐标均为整数的点).
(1)求数列{a
n}的通项公式;
(2)记数列{a
n}的前n项和为S
n,且T
n=
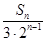
.若对于一切的正整数n,总有T
n≤m,求实数m的取值范围.
题号:936641
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】已知数列{a
n}满足a
1+a
2+…+a
n=n
2(n∈N
*).
(1)求数列{a
n}的通项公式;
(2)对任意给定的k∈N
*,是否存在p,r∈N
*(k<p<r)使
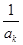
,
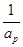
,
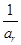
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
题号:936647
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】正项数列{a
n}的前项和满足:
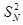
-(n
2+n-1)S
n-(n
2+n)=0.
(1)求数列{a
n}的通项公式a
n;
(2)令b
n=
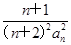
,数列{b
n}的前n项和为T
n.证明:对于任意的n∈N
*,都有T
n<
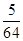
.
题号:936648
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】设{a
n}是首项为a,公差为d的等差数列(d≠0),S
n是其前n项和.记b
n=
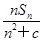
,n∈N
*,其中c为实数.
(1)若c=0,且b
1,b
2,b
4成等比数列,证明:S
nk=n
2S
k(k,n∈N
*);
(2)若{b
n}是等差数列,证明:c=0.
题号:936649
题型:解答题
难易度:困难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】已知数列{a
n}中,a
1=2,n∈N
*,a
n>0,数列{a
n}的前n项和为S
n,且满足a
n+1=
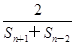
.
(1)求{S
n}的通项公式;
(2)设{b
k}是{S
n}中的按从小到大顺序组成的整数数列.
①求b
3;
②存在N(N∈N
*),当n≤N时,使得在{S
n}中,数列{b
k}有且只有20项,求N的范围.
题号:936650
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】设数列{a
n}的前n项和为S
n.已知a
1=1,
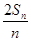
=a
n+1-
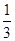
n
2-n-
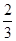
,n∈N
*.
(1)求a
2的值;
(2)求数列{a
n}的通项公式;
(3)证明:对一切正整数n,有
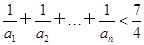
.
题号:936651
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】已知数列a
n=n-16,b
n=(-1)
n|n-15|,其中n∈N
*.
(1)求满足a
n+1=|b
n|的所有正整数n的集合;
(2)若n≠16,求数列
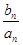
的最大值和最小值;
(3)记数列{a
nb
n}的前n项和为S
n,求所有满足S
2m=S
2n(m<n)的有序整数对(m,n).
题号:936672
题型:解答题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(带解析)
【题文】设无穷数列{an}满足:n∈Ν,an<an+1,an∈N.记bn=aan,cn=aan+1(n∈N*).
(1)若bn=3n(n∈N*),求证:a1=2,并求c1的值;
(2)若{cn}是公差为1的等差数列,问{an}是否为等差数列,证明你的结论.
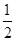 ,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.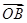 =a100·
=a100·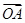 +a101
+a101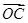 ,且A、B、C三点共线(该直线不过点O),则S200=________.
,且A、B、C三点共线(该直线不过点O),则S200=________.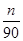 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.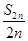 =2013,求n的值;
=2013,求n的值;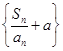 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+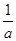 .
.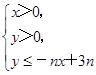 所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).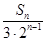 .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.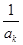 ,
,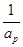 ,
,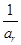 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.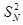 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.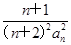 ,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<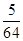 .
.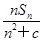 ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.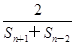 .
.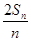 =an+1-
=an+1-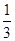 n2-n-
n2-n-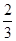 ,n∈N*.
,n∈N*.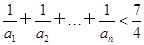 .
.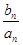 的最大值和最小值;
的最大值和最小值;