适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-05题数:12
提示:单击题文可显示答案与解析。
题号:939848
题型:选择题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】定义在R上的函数的图象关于点
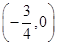
成中心对称,且对任意的实数x都有f(x)=-f
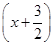
,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2013)=( )
题号:939849
题型:选择题
难易度:较易
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】函数
f(
x)的图象向右平移1个单位长度,所得图象与曲线
y=e
x关于
y轴对称,则
f(
x)=( )
| A.ex+1 | B.ex-1 | C.e-x+1 | D.e-x-1 |
题号:939850
题型:选择题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】已知偶函数f(x)当x∈[0,+∞)时是单调递增函数,则满足f(
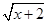
)<f(x)的x的取值范围是( )
| A.(2,+∞) | B.(-∞,-1) |
| C.[-2,-1)∪(2,+∞) | D.(-1,2) |
题号:939851
题型:选择题
难易度:较易
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】设函数f(x)=
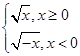
若f(a)+f(-1)=2,则a=( )
题号:4186960
题型:选择题
难易度:较易
日期:2014-04-06
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】x为实数,[x]表示不超过x的最大整数,则函数f(x)=x-[x]在R上为( )
题号:4186961
题型:选择题
难易度:一般
日期:2014-04-06
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】已知函数f(x)=x
2-2(a+2)x+a
2,g(x)=-x
2+2(a-2)x-a
2+8.设H
1(x)=max{f(x),g(x)},H
2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H
1(x)的最小值为A,H
2(x)的最大值为B,则A-B=( )
| A.16 | B.-16 |
| C.a2-2a-16 | D.a2+2a-16 |
题号:939845
题型:填空题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】对于定义在R上的函数f(x)有以下五个命题:
①若y=f(x)是奇函数,则y=f(x-1)的图象关于A(1,0)对称;
②若对于任意x∈R,有f(x-1)=f(x+1),则f(x)关于直线x=1对称;
③函数y=f(x+1)与y=f(1-x)的图象关于直线x=1对称;
④如果函数y=f(x)满足f(x+1)=f(1-x),f(x+3)=f(3-x),那么该函数以4为周期.
其中正确命题的序号为________.
题号:939846
题型:填空题
难易度:较易
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】设函数f(x)=
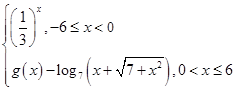
若f(x)是奇函数,则g(3)=________.
题号:939847
题型:填空题
难易度:较易
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】若函数f(x)=x2-|x+a|为偶函数,则实数a=________.
题号:939843
题型:解答题
难易度:较难
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】已知函数f(x)=ex-e-x(x∈R且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.
题号:939844
题型:解答题
难易度:较难
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】已知函数f(x)=x
2+
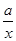
(x≠0,a∈R).
(1)判断函数f(x)的奇偶性;
(2)若f(x)在区间[2,+∞)上是增函数,求实数a的取值范围.
题号:4186962
题型:解答题
难易度:较难
日期:2014-04-06
来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(带解析)
【题文】对定义域分别是D
f,D
g的函数y=f(x),y=g(x),规定:函数h(x)=
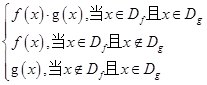
(1)若函数f(x)=
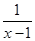
,g(x)=x
2,写出函数h(x)的解析式;
(2)求问题(1)中函数h(x)的值域.
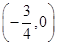 成中心对称,且对任意的实数x都有f(x)=-f
成中心对称,且对任意的实数x都有f(x)=-f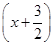 ,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2013)=( )
,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2013)=( )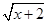 )<f(x)的x的取值范围是( )
)<f(x)的x的取值范围是( )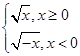 若f(a)+f(-1)=2,则a=( )
若f(a)+f(-1)=2,则a=( )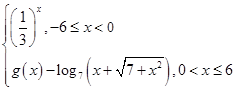 若f(x)是奇函数,则g(3)=________.
若f(x)是奇函数,则g(3)=________.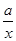 (x≠0,a∈R).
(x≠0,a∈R).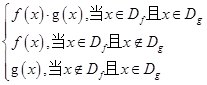
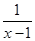 ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;