适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-03题数:11
提示:单击题文可显示答案与解析。
题号:940795
题型:选择题
难易度:一般
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】执行如图所示的程序框图,如果依次输入函数:
f(
x)=3
x、
f(
x)=sin
x、
f(
x)=
x3、
f(
x)=
x+
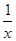
,那么输出的函数
f(
x)为( )
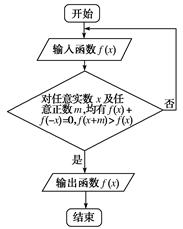
| A.3x | B.sin x | C.x3 | D.x+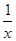 |
题号:940796
题型:选择题
难易度:较难
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】若数列{
an}是等差数列,则数列{
bn}
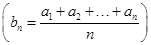
也为等差数列.类比这一性质可知,若正项数列{
cn}是等比数列,且{
dn}也是等比数列,则
dn的表达式应为( )
题号:940797
题型:选择题
难易度:容易
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
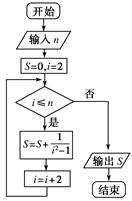
【题文】)执行如图所示的程序框图,若输入
n=10,则输出
S=( )
题号:4187032
题型:选择题
难易度:容易
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数
M的值是( )

题号:4187033
题型:选择题
难易度:容易
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】阅读如下程序框图,如果输出
i=4,那么空白的判断框中应填入的条件是( )

题号:940792
题型:填空题
难易度:一般
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】已知命题:若数列{
an}为等差数列,且
am=
a,
an=
b(
m≠
n,
m、
n∈N
*),则
am+n=
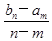
;现已知等比数列{
bn}(
bn>0,
n∈N
*),
bm=
a,
bn=
b(
m≠
n,
m、
n∈N
*),若类比上述结论,则可得到
bm+n=________.
题号:940793
题型:填空题
难易度:较易
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】已知函数
f(
x)=
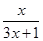
,对于数列{
an}有
an=
f(
an-1)(
n∈N
*,且
n≥2),如果
a1=1,那么
a2=________.
an=________.
题号:940794
题型:填空题
难易度:较易
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
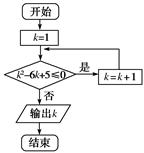
【题文】如图是一个算法流程图,则输出的
k的值是________.
题号:940770
题型:解答题
难易度:一般
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】根据如图所示的程序框图,将输出的
x,
y值依次分别记为
x1,
x2,…,
xk,…;
y1,
y2,…,
yk,….
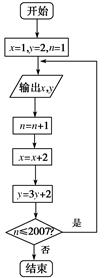
(1)分别求数列{
xk}和{
yk}的通项公式;
(2)令
zk=
xkyk,求数列{
zk}的前
k项和
Tk,其中
k∈N
*,
k≤2 007.
题号:940771
题型:解答题
难易度:一般
日期:2014-04-03
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】观察下列三角形数表,假设第
n行的第二个数为
an(
n≥2,
n∈N
*).

(1)依次写出第六行的所有6个数;
(2)归纳出
an+1与
an的关系式并求出{
an}的通项公式.
题号:4187034
题型:解答题
难易度:一般
日期:2014-04-04
来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(带解析)
【题文】某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin 13°cos 17°;
②sin215°+cos215°-sin 15°cos 15°;
③sin218°+cos212°-sin 18°cos 12°;
④sin2(-18°)+cos248°-sin(-18°)cos 48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos 55°.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
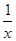 ,那么输出的函数f(x)为( )
,那么输出的函数f(x)为( )
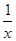
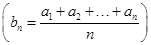 也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )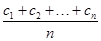
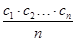

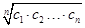

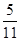
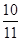

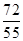


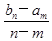 ;现已知等比数列{bn}(bn>0,n∈N*),bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n=________.
;现已知等比数列{bn}(bn>0,n∈N*),bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n=________.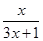 ,对于数列{an}有an=f(an-1)(n∈N*,且n≥2),如果a1=1,那么a2=________.an=________.
,对于数列{an}有an=f(an-1)(n∈N*,且n≥2),如果a1=1,那么a2=________.an=________.

