适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-13题数:11
提示:单击题文可显示答案与解析。
题号:949462
题型:选择题
难易度:一般
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知定义在R上的函数
y=
f(
x)满足以下三个条件:①对于任意的
x∈R,都有
f(
x+4)=
f(
x);②对于任意的
x1,
x2∈R,且0≤
x1<
x2≤2,都有
f(
x1)<
f(
x2);③函数
y=
f(
x+2)的图象关于
y轴对称.则下列结论中正确的是( ).
| A.f(4.5)<f(7)<f(6.5) | B.f(7)<f(4.5)<f(6.5) |
| C.f(7)<f(6.5)<f(4.5) | D.f(4.5)<f(6.5)<f(7) |
题号:949463
题型:选择题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知
x,
y为正实数,则( ).
| A.2lg x+lg y=2lg x+2lg y | B.2lg(x+y)=2lg x·2lg y |
| C.2lg x·lg y=2lg x+2lg y | D.2lg(xy)=2lg x·2lg y |
题号:949464
题型:选择题
难易度:一般
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】函数
f(
x)=log
2|
x|,
g(
x)=-
x2+2,则
f(
x)·
g(
x)的图象只可能是 ( ).
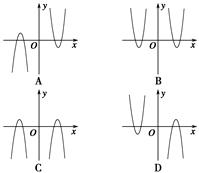
题号:949465
题型:选择题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】设函数
f(
x)=
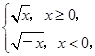
若
f(
a)+
f(-1)=2,则
a等于( ).
题号:4187970
题型:选择题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】同时满足两个条件:①定义域内是减函数;②定义域内是奇函数的函数是( ).
| A.f(x)=-x|x| | B.f(x)=x3 |
| C.f(x)=sin x | D.f(x)=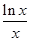 |
题号:947873
题型:填空题
难易度:较易
日期:2014-03-22
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知f(x)=ln(1+x)的定义域为集合M,g(x)=2x+1的值域为集合N,则M∩N=________.
题号:4187638
题型:填空题
难易度:较易
日期:2014-03-22
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知函数f(x)=x3+x,对任意的m∈[-2,2],f(mx-2)+f(x)<0恒成立,则x的取值范围是________.
题号:4187972
题型:填空题
难易度:较难
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知函数
y=
f(
x)是R上的偶函数,对∀
x∈R都有
f(
x+4)=
f(
x)+
f(2)成立.当
x1,
x2∈[0,2],且
x1≠
x2时,都有
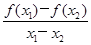
<0,给出下列命题:
①
f(2)=0;
②直线
x=-4是函数
y=
f(
x)图象的一条对称轴;
③函数
y=
f(
x)在[-4,4]上有四个零点;
④
f(2 014)=0.
其中所有正确命题的序号为________.
题号:947867
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知函数f(x)=ex-e-x(x∈R且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.
题号:947869
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点对称的点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
题号:4187973
题型:解答题
难易度:较难
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(带解析)
【题文】已知二次函数
f(
x)=
ax2+
bx+1(
a>0),
F(
x)=
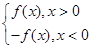
若
f(-1)=0,且对任意实数
x均有
f(
x)≥0成立.
(1)求
F(
x)的表达式;
(2)当
x∈[-2,2]时,
g(
x)=
f(
x)-
kx是单调函数,求
k的取值范围.

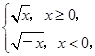 若f(a)+f(-1)=2,则a等于( ).
若f(a)+f(-1)=2,则a等于( ).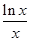
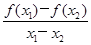 <0,给出下列命题:
<0,给出下列命题: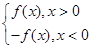 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.