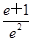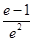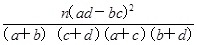适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-26题数:13
提示:单击题文可显示答案与解析。
题号:946126
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】在区间[1,5]和[2,6]内分别取一个数,记为
a和
b,则方程
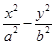
=1(
a<
b)表示离心率小于
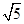
的双曲线的概率为( )
题号:946127
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】甲、乙两位射击运动员,甲击中环数
X1~
B(10,0.9),乙击中环数
X2=2
Y+1,其中
Y~
B(5,0.8),那么下列关于甲、乙两运动员平均击中环数的说法正确的是( )
| A.甲平均击中的环数比乙平均击中的环数多 |
| B.乙平均击中的环数比甲平均击中的环数多 |
| C.甲、乙两人平均击中的环数相等 |
| D.仅依据上述数据,无法判断谁击中的环数多 |
题号:946128
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】已知某随机变量
X的概率密度函数为
P(
x)=
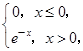
则随机变量
X落在区间(1,2)内的概率为( )
| A.e2+e | B.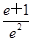 | C.e2-e | D.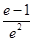 |
题号:946129
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】将容量为
n的样本中的数据分成6组,若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则
n的值为( )
题号:946130
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】如果随机变量
X~
N(-1,
σ2),且
P(-3≤
X≤-1)=0.4,则
P(
X≥1)=( )
题号:946131
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
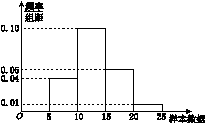
【题文】某个小区住户共200户,为调查小区居民的7月份用水量,用分层抽样的方法抽取了50户进行调查,得到本月的用水量(单位:m
3)的频率分布直方图如图所示,则小区内用水量超过15 m
3的住户的户数为( )
题号:932967
题型:填空题
难易度:较易
日期:2014-04-20
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
运动员
| 第1次
| 第2次
| 第3次
| 第4次
| 第5次
|
甲
| 87
| 91
| 90
| 89
| 93
|
乙
| 89
| 90
| 91
| 88
| 92
|
则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.
题号:946124
题型:填空题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】有20个零件,其中16个一等品,4个二等品,若从这20个零件中任意取3个,那么至少有1个一等品的概率是________.
题号:946125
题型:填空题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】甲、乙、丙三人参加某项测试,他们能达标的概率分别是0.8,0.6,0.5,则三人中至少有一人达标的概率是________.
题号:4187468
题型:填空题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】一个家庭中有两个小孩.假定生男、生女是等可能的,已知这个家庭有一个是女孩,则这时另一个小孩是男孩的概率是________.
题号:946121
题型:解答题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】在一次数学测验后,班级学委对选答题的选题情况进行了统计,如下表:
| 几何证明选讲
| 坐标系与
参数方程
| 不等式选讲
| 合计
|
男同学(人数)
| 12
| 4
| 6
| 22
|
女同学(人数)
| 0
| 8
| 12
| 20
|
合计
| 12
| 12
| 18
| 42
|
(1)在统计结果中,如果把几何证明选讲和坐标系与参数方程称为几何类,把不等式选讲称为代数类,我们可以得到如下2×2列联表:
| 几何类
| 代数类
| 总计
|
男同学(人数)
| 16
| 6
| 22
|
女同学(人数)
| 8
| 12
| 20
|
总计
| 24
| 18
| 42
|
据此统计你是否认为选做“几何类”或“代数类”与性别有关?若有关,你有多大的把握?
(2)在原统计结果中,如果不考虑性别因素,按分层抽样的方法从选做不同选做题的同学中随机选出7名同学进行座谈.已知这名班级学委和两名数学科代表都在选做“不等式选讲”的同学中.
①求在这名班级学委被选中的条件下,两名数学科代表也被选中的概率;
②记抽到数学科代表的人数为
X,求
X的分布列及数学期望
E(
X).
下面临界值表仅供参考:
P(K2≥k0)
| 0.15
| 0.10
| 0.05
| 0.025
| 0.010
| 0.005
| 0.001
|
k0
| 2.072
| 2.706
| 3.841
| 5.024
| 6.635
| 7.879
| 10.828
|
参考公式:
K2=
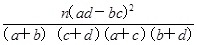
题号:946122
题型:解答题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别
| PM2.5(微克/立方米)
| 频数(天)
| 频率
|
第一组
| (0,15]
| 4
| 0.1
|
第二组
| (15,30]
| 12
| 0.3
|
第三组
| (30,45]
| 8
| 0.2
|
第四组
| (45,60]
| 8
| 0.2
|
第五组
| (60,75]
| 4
| 0.1
|
第六组
| (75,90)
| 4
| 0.1
|
(1)写出该样本的众数和中位数(不必写出计算过程);
(2)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(3)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为
X,求
X的分布列及数学期望
E(
X).
题号:946123
题型:解答题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(带解析)
【题文】某种报纸,进货商当天以每份1元从报社购进,以每份2元售出.若当天卖不完,剩余报纸报社以每份0.5元的价格回收.根据市场统计,得到这个季节的日销售量
X(单位:份)的频率分布直方图(如图所示),将频率视为概率.
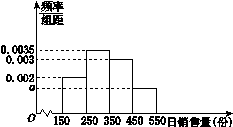
(1)求频率分布直方图中
a的值;
(2)若进货量为
n(单位:份),当
n≥
X时,求利润
Y的表达式;
(3)若当天进货量
n=400,求利润
Y的分布列和数学期望
E(
Y)(统计方法中,同一组数据常用该组区间的中点值作为代表).
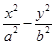 =1(a<b)表示离心率小于
=1(a<b)表示离心率小于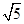 的双曲线的概率为( )
的双曲线的概率为( )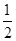
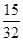
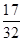
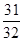
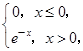 则随机变量X落在区间(1,2)内的概率为( )
则随机变量X落在区间(1,2)内的概率为( )