适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-13题数:11
提示:单击题文可显示答案与解析。
题号:949398
题型:选择题
难易度:较难
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】已知
f(
x)是定义在(0,+∞) 上的非负可导函数,且满足
xf′(
x)+
f(
x)≤0,对任意的0<
a<
b,则必有( ).
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D.bf(b)≤f(a) |
题号:949399
题型:选择题
难易度:一般
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】函数
f(
x)的定义域是R,
f(0)=2,对任意
x∈R,
f(
x)+
f′(
x)>1,则不等式e
x·
f(
x)>e
x+1的解集为( ).
题号:949400
题型:选择题
难易度:一般
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
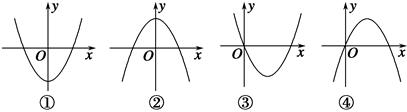
【题文】下面四个图象中,有一个是函数
f(
x)=
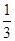 x3
x3+
ax2+(
a2-1)
x+1(
a∈R)的导函数
y=
f′(
x)图象,则
f(-1)等于( ).
题号:949401
题型:选择题
难易度:较难
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】已知函数
f(
x)=
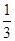 x3
x3-2
x2+3
m,
x∈[0,+∞),若
f(
x)+5≥0恒成立,则实数
m的取值范围是( )
A.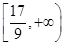 | B.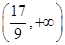 |
| C.(-∞,2] | D.(-∞,2) |
题号:4187935
题型:选择题
难易度:一般
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】设函数
f(
x)满足
x2f′(
x)+2
xf(
x)=
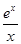
,
f(2)=
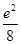
,则
x>0时,
f(
x)( ).
| A.有极大值,无极小值 |
| B.有极小值,无极大值 |
| C.既有极大值又有极小值 |
| D.既无极大值也无极小值 |
题号:947813
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】关于x的方程x3-3x2-a=0有三个不同的实数解,则实数a的取值范围是________.
题号:949396
题型:填空题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】若函数
f(
x)=-
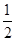 x2
x2+4
x-3ln
x在[
t,
t+1]上不单调,则
t的取值范围是______.
题号:4187936
题型:填空题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】已知函数
f(
x)=
x-
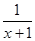
,
g(
x)=
x2-2
ax+4,若任意
x1∈[0,1],存在
x2∈[1,2],使
f(
x1)≥
g(
x2),则实数
a的取值范围是______.
题号:3883853
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
题号:4187631
题型:解答题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】已知x=3是函数f(x)=aln(1+x)+x2-10x的一个极值点.
(1)求a;
(2)求函数f(x)的单调区间;
(3)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
题号:4187937
题型:解答题
难易度:较难
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(带解析)
【题文】设函数f(x)=ax-(1+a2)x2,其中a>0,区间I={x|f(x)>0}.
(1)求I的长度(注:区间(α,β)的长度定义为β-α);
(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I长度的最小值.
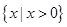
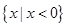

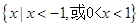
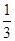 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于( ).
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于( ).
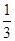
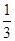
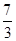
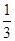 或
或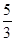
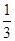 x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是( )
x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是( )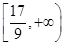
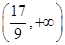
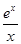 ,f(2)=
,f(2)=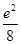 ,则x>0时,f(x)( ).
,则x>0时,f(x)( ).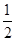 x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是______.
x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是______.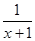 ,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.
,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.