适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:6
提示:单击题文可显示答案与解析。
题号:950612
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-5练习卷(带解析)
【题文】已知椭圆
C:
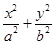
=1(
a>
b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线
l:
x-
y+
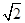
=0与以原点为圆心, 以椭圆
C的短半轴长为半径的圆相切.
(1)求椭圆
C的方程;
(2)设
M是椭圆的上顶点,过点
M分别作直线
MA,
MB交椭圆于
A,
B两点,设两直线的斜率分别为
k1,
k2,且
k1+
k2=4,证明:直线
AB过定点
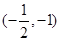
.
题号:950613
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-5练习卷(带解析)
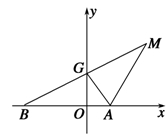
【题文】已知定点
A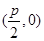
(
p为常数,
p>0),
B为
x轴负半轴上的一个动点,动点
M使得|
AM|=|
AB|,且线段
BM的中点
G在
y轴上.
(1)求动点
M的轨迹
C的方程;
(2)设
EF为曲线
C的一条动弦(
EF不垂直于
x轴),其垂直平分线与
x轴交于点
T(4,0),当
p=2时,求|
EF|的最大值.
题号:950614
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-5练习卷(带解析)
【题文】设
A(
x1,
y1),
B(
x2,
y2)是椭圆
C:
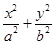
=1(
a>
b>0)上两点,已知
m=
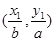
,
n=
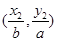
,若
m·
n=0且椭圆的离心率
e=
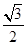
,短轴长为2,
O为坐标原点.
(1)求椭圆的方程;
(2)试问△
AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
题号:950615
题型:解答题
难易度:困难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-5练习卷(带解析)
【题文】已知动点
P到点
A(-2,0)与点
B(2,0)的斜率之积为-
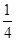
,点
P的轨迹为曲线
C.
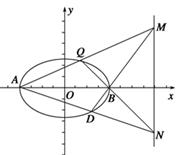
(1)求曲线
C的方程;
(2)若点
Q为曲线
C上的一点,直线
AQ,
BQ与直线
x=4分别交于
M,
N两点,直线
BM与椭圆的交点为
D.求证,
A,
D,
N三点共线.
题号:950616
题型:解答题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-5练习卷(带解析)
【题文】在平面直角坐标系
xOy中,动点
P到直线
l:
x=2的距离是到点
F(1,0)的距离的
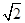
倍.
(1)求动点
P的轨迹方程;
(2)设直线
FP与(1)中曲线交于点
Q,与
l交于点
A,分别过点
P和
Q作
l的垂线,垂足为
M,
N,问:是否存在点
P使得△
APM的面积是△
AQN面积的9倍?若存在,求出点
P的坐标;若不存在,说明理由.
题号:950617
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-5练习卷(带解析)
【题文】已知椭圆
C1:
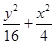
=1,椭圆
C2以
C1的短轴为长轴,且与
C1有相同的离心率.
(1)求椭圆
C2的方程;
(2)设直线
l与椭圆
C2相交于不同的两点
A、
B,已知
A点的坐标为(-2,0),点
Q(0,
y0)在线段
AB的垂直平分线上,且
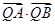
=4,求直线
l的方程.
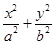 =1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+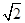 =0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
=0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.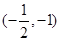 .
.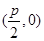 (p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
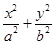 =1(a>b>0)上两点,已知m=
=1(a>b>0)上两点,已知m=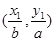 ,n=
,n=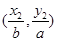 ,若m·n=0且椭圆的离心率e=
,若m·n=0且椭圆的离心率e=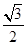 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.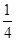 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
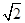 倍.
倍.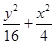 =1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.
=1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.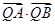 =4,求直线l的方程.
=4,求直线l的方程.