适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:10
提示:单击题文可显示答案与解析。
题号:951056
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】下列命题中错误的是 ( ).
| A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β |
| B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
| C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ |
| D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β |
题号:4188151
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是( ).
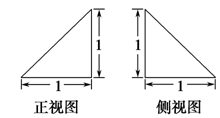
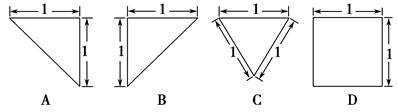
题号:4188152
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( ).
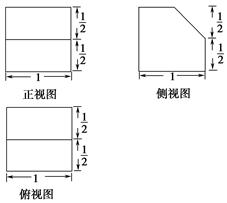
题号:4188153
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】设三棱柱的侧棱垂直于底面,所有棱的长都为
a,顶点都在一个球面上,则该球的表面积为 ( ).
| A.πa2 | B.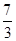 πa2 πa2 | C.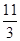 πa2 πa2 | D.5πa2 |
题号:4188154
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】如图,在正方形
ABCD中,
E、
F分别是
BC、
CD的中点,
AC∩
EF=
G.现在沿
AE、
EF、
FA把这个正方形折成一个四面体,使
B、
C、
D三点重合,重合后的点记为
P,则在四面体
P-
AEF中必有 ( ).
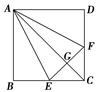
| A.AP⊥△PEF所在平面 |
| B.AG⊥△PEF所在平面 |
| C.EP⊥△AEF所在平面 |
| D.PG⊥△AEF所在平面 |
题号:951055
题型:填空题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
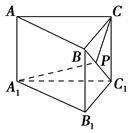
【题文】如图所示,在直三棱柱
ABC-A1B1C1中,底面为直角三角形,∠
ACB=90°,
AC=6,
BC=
CC1=
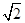
,
P是
BC1上一动点,则
CP+
PA1的最小值是________.
题号:4188155
题型:填空题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为________.
题号:4188156
题型:填空题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
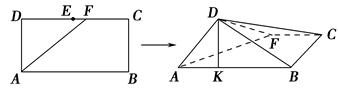
【题文】如图,在长方形
ABCD中,
AB=2,
BC=1,
E为
DC的中点,
F为线段
EC(端点除外)上一动点,现将△
AFD沿
AF折起,使平面
ABD⊥平面
ABC.在平面
ABD内过点
D作
DK⊥
AB,
K为垂足.设
AK=
t,则
t的取值范围是________.
题号:951054
题型:解答题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】如图,在直四棱柱
ABCD-A1B1C1D1中,底面
ABCD为等腰梯形,
AB∥
CD,
AB=4,
BC=
CD=2,
AA1=2,
E,
E1,
F分别是棱
AD,
AA1,
AB的中点.
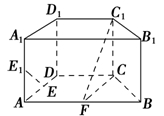
(1)证明:直线
EE1∥平面
FCC1;
(2)求二面角
B-FC1-
C的余弦值.
题号:4188157
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(带解析)
【题文】如图,四棱锥
P-ABCD中,
PA⊥底面
ABCD,
AB⊥
AD,点
E在线段
AD上,且
CE∥
AB.
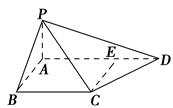
(1)求证:
CE⊥平面
PAD;
(2)若
PA=
AB=1,
AD=3,
CD=
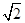
,∠
CDA=45°,求四棱锥
P-ABCD的体积.



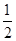 cm3
cm3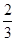 cm3
cm3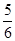 cm3
cm3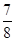 cm3
cm3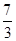 πa2
πa2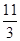 πa2
πa2
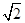 ,P是BC1上一动点,则CP+PA1的最小值是________.
,P是BC1上一动点,则CP+PA1的最小值是________.



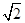 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.