适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-01题数:4
提示:单击题文可显示答案与解析。
题号:941302
题型:解答题
难易度:一般
日期:2014-04-01
来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(带解析)
【题文】已知
x0,
x0+
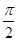
是函数
f(
x)=cos
2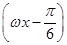
-sin
2ωx(
ω>0)的两个相邻的零点.
(1)求
f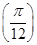
的值;
(2)若对∀
x∈
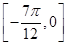
,都有|
f(
x)-
m|≤1,求实数
m的取值范围.
题号:941303
题型:解答题
难易度:一般
日期:2014-04-01
来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(带解析)
【题文】已知向量
a=(cos
α,sin
α),
b=(cos
x,sin
x),
c=(sin
x+2sin
α,cos
x+2cos
α),其中0<
α<
x<π.
(1)若
α=
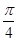
,求函数
f(
x)=
b·
c的最小值及相应
x的值;
(2)若
a与
b的夹角为
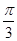
,且
a⊥
c,求tan 2
α的值.
题号:941304
题型:解答题
难易度:一般
日期:2014-04-01
来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(带解析)
【题文】已知函数
f(
x)=2
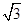
sin(2
ωx+
φ)(
ω>0,
φ∈(0,π))的图象中相邻两条对称轴间的距离为
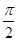
,且点
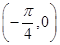
是它的一个对称中心.
(1)求
f(
x)的表达式;
(2)若
f(
ax)(
a>0)在
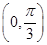
上是单调递减函数,求
a的最大值.
题号:941305
题型:解答题
难易度:较难
日期:2014-04-01
来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(带解析)
【题文】已知函数
f(
x)=2sin
xcos
x+2
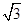
cos
2x-
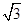
,
x∈R.
(1)求函数
f(
x)的最小正周期;
(2)在锐角△
ABC中,若
f(
A)=1,
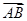
·
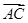
=
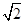
,求△
ABC的面积.
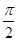 是函数f(x)=cos2
是函数f(x)=cos2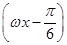 -sin2ωx(ω>0)的两个相邻的零点.
-sin2ωx(ω>0)的两个相邻的零点.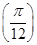 的值;
的值;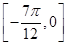 ,都有|f(x)-m|≤1,求实数m的取值范围.
,都有|f(x)-m|≤1,求实数m的取值范围.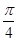 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;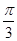 ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值.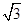 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为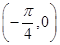 是它的一个对称中心.
是它的一个对称中心.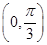 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.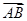 ·
·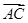 =
=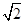 ,求△ABC的面积.
,求△ABC的面积.