适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:6
提示:单击题文可显示答案与解析。
题号:950624
题型:解答题
难易度:困难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-3练习卷(带解析)
【题文】在等腰梯形
ABCD中,
AD∥
BC,
AD=
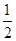 BC
BC,∠
ABC=60°,
N是
BC的中点,将梯形
ABCD绕
AB旋转90°,得到梯形
ABC′
D′(如图).
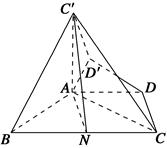
(1)求证:
AC⊥平面
ABC′;
(2)求证:
C′
N∥平面
ADD′;
(3)求二面角
A-C′
N-C的余弦值.
题号:950625
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-3练习卷(带解析)
【题文】如图,在四棱锥
P-ABCD中,平面
PAC⊥平面
ABCD,且
PA⊥
AC,
PA=
AD=2.四边形
ABCD满足
BC∥
AD,
AB⊥
AD,
AB=
BC=1.点
E,
F分别为侧棱
PB,
PC上的点,且
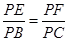
=
λ.
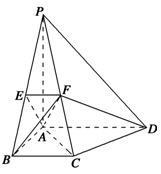
(1)求证:
EF∥平面
PAD.
(2)当
λ=
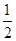
时,求异面直线
BF与
CD所成角的余弦值;
(3)是否存在实数
λ,使得平面
AFD⊥平面
PCD?若存在,试求出
λ的值;若不存在,请说明理由.
题号:950626
题型:解答题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-3练习卷(带解析)
【题文】在正三棱柱
ABC-A1B1C1中,
AB=2,
AA1=
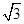
,点
D为
AC的中点,点
E在线段
AA1上.
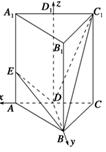
(1)当
AE∶
EA1=1∶2时,求证
DE⊥
BC1;
(2)是否存在点
E,使二面角
D-BE-A等于60°,若存在求
AE的长;若不存在,请说明理由.
题号:950627
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-3练习卷(带解析)
【题文】如图,四边形
ABCD为矩形,
PD⊥平面
ABCD,
PD∥
QA,
QA=
AD=
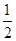 PD
PD.
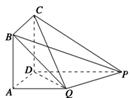
(1)求证:平面
PQC⊥平面
DCQ;
(2)若二面角
Q-BP-C的余弦值为-
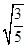
,求
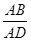
的值.
题号:950628
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-3练习卷(带解析)
【题文】如图,直三棱柱
ABC-A1B1C1中,△
ABC是等边三角形,
D是
BC的中点.
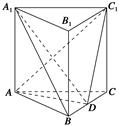
(1)求证:
A1B∥平面
ADC1;
(2)若
AB=
BB1=2,求
A1D与平面
AC1D所成角的正弦值.
题号:4188105
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-3练习卷(带解析)
【题文】已知四棱锥
P-ABCD的底面
ABCD是等腰梯形,
AB∥
CD,且
AC⊥
BD,
AC与
BD交于
O,
PO⊥底面
ABCD,
PO=2,
AB=2
CD=2
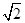
,
E,
F分别是
AB,
AP的中点.
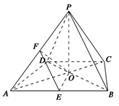
(1)求证:
AC⊥
EF;
(2)求二面角
F-OE-A的余弦值.
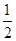 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
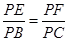 =λ.
=λ.
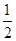 时,求异面直线BF与CD所成角的余弦值;
时,求异面直线BF与CD所成角的余弦值;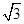 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.
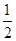 PD.
PD.
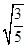 ,求
,求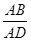 的值.
的值.
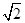 ,E,F分别是AB,AP的中点.
,E,F分别是AB,AP的中点.