适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:6
提示:单击题文可显示答案与解析。
题号:950529
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(带解析)
【题文】已知函数f(x)=(ax2+bx+c)ex且f(0)=1,f(1)=0.
(1)若f(x)在区间[0,1]上单调递减,求实数a的取值范围;
(2)当a=0时,是否存在实数m使不等式2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立?若存在,求出m的值,若不存在,请说明理由.
题号:950530
题型:解答题
难易度:困难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(带解析)
【题文】已知抛物线
C:
y2=2
px(
p>0),
M点的坐标为(12,8),
N点在抛物线
C上,且满足
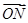
=
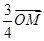
,
O为坐标原点.
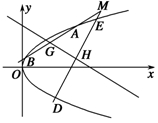
(1)求抛物线
C的方程;
(2)以
M点为起点的任意两条射线
l1,
l2的斜率乘积为1,并且
l1与抛物线
C交于
A,
B两点,
l2与抛物线
C交于
D,
E两点,线段
AB,
DE的中点分别为
G,
H两点.求证:直线
GH过定点,并求出定点坐标.
题号:950531
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(带解析)
【题文】如图,在矩形
ABCD中,
AB=2
AD=2,
O为
CD的中点,沿
AO将△
AOD折起,使
DB=
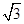
.
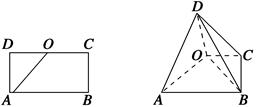
(1)求证:平面
AOD⊥平面
ABCO;
(2)求直线
BC与平面
ABD所成角的正弦值.
题号:950572
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(带解析)
【题文】已知数列{
an}满足
a1=3,
an+1=
an+
p·3
n(
n∈N
*,
p为常数),
a1,
a2+6,
a3成等差数列.
(1)求
p的值及数列{
an}的通项公式;
(2)设数列{
bn}满足
bn=
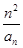
,证明:
bn≤
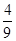
.
题号:950573
题型:解答题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(带解析)
【题文】一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5;4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(I)求取出的3个球编号都不相同的概率;
(II)记
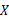
为取出的3个球中编号的最小值,求
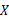
的分布列与数学期望.
题号:950574
题型:解答题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(带解析)
【题文】已知函数
f(
x)=
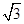
sin
xcos
x+cos
2x-
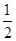
,△
ABC三个内角
A,
B,
C的对边分别为
a,
b,
c,且
f(
B)=1.
(1)求角
B的大小;
(2)若
a=
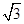
,
b=1,求
c的值.
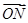 =
=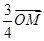 ,O为坐标原点.
,O为坐标原点.
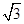 .
.
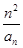 ,证明:bn≤
,证明:bn≤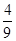 .
.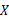 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求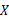 的分布列与数学期望.
的分布列与数学期望.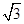 sin xcos x+cos 2x-
sin xcos x+cos 2x-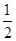 ,△ABC三个内角A,B,C的对边分别为a,b,c,且f(B)=1.
,△ABC三个内角A,B,C的对边分别为a,b,c,且f(B)=1.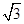 ,b=1,求c的值.
,b=1,求c的值.