适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2009年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2009年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2009年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2009年')}}上传日期:2010-03-30题数:17
提示:单击题文可显示答案与解析。
题号:1333196
题型:选择题
难易度:较难
日期:2010-03-11
来源:2009高考真题汇编5-平面向量
【题文】设
P是△
ABC所在平面内的一点,
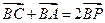
,则( )
题号:1440158
题型:选择题
难易度:较易
日期:2009-11-28
来源:2009高考真题汇编5-平面向量
【题文】已知平面向量
a=
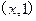
,
b=
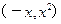
,则向量

( )
A平行于
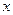
轴 B.平行于第一、三象限的角平分线
C.平行于
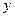
轴 D.平行于第二、四象限的角平分线
题号:1440693
题型:选择题
难易度:容易
日期:2009-11-26
来源:2009高考真题汇编5-平面向量
【题文】已知三角形的三边长分别为

,则它的边与半径为
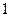
的圆的公共点个数最多为( )
题号:1440696
题型:选择题
难易度:较易
日期:2009-11-26
来源:2009高考真题汇编5-平面向量
题号:1441045
题型:选择题
难易度:一般
日期:2009-11-26
来源:2009高考真题汇编5-平面向量
【题文】设向量
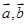
满足:
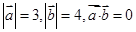
.以
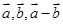
的模为边长构成三角形,则它的边与半径为

的圆的公共点个数最多为 ( )
题号:1443341
题型:选择题
难易度:容易
日期:2009-11-23
来源:2009高考真题汇编5-平面向量
【题文】在平行四边形ABCD中,AC为一条对角线,若
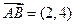
,
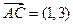
,则
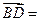
( )
| A.(-2,-4) | B.(-3,-5) | C.(3,5) | D.(2,4) |
题号:1448534
题型:选择题
难易度:容易
日期:2009-11-15
来源:2009高考真题汇编5-平面向量
题号:1449038
题型:选择题
难易度:一般
日期:2009-11-14
来源:2009高考真题汇编5-平面向量
题号:3767441
题型:选择题
难易度:容易
日期:2012-07-25
来源:2009高考真题汇编5-平面向量
【题文】已知O,N,P在
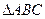
所在平面内,且
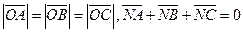
,且
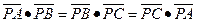
,则点O,N,P依次是
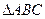
的( )
| A.重心外心垂心 | B.重心外心内心 |
| C.外心重心垂心 | D.外心重心内心 |
(注:三角形的三条高线交于一点,此点为三角型的垂心)
题号:1327845
题型:填空题
难易度:一般
日期:2010-03-22
来源:2009高考真题汇编5-平面向量
题号:1332471
题型:填空题
难易度:一般
日期:2010-03-13
来源:2009高考真题汇编5-平面向量
【题文】如图2,两块斜边长相等的直角三角板拼在一起,若
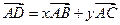
,则
x=
,
y=
。

题号:1439113
题型:填空题
难易度:容易
日期:2009-11-30
来源:2009高考真题汇编5-平面向量
【题文】在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为___________.
题号:3767619
题型:填空题
难易度:容易
日期:2013-07-01
来源:2009高考真题汇编5-平面向量
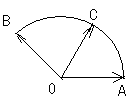
【题文】给定两个长度为1的平面向量
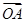
和

,它们的夹角为
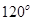
.如图所示,点C在以O为圆心的圆弧
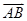
上变动.若
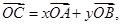
其中
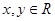
,则
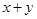
的最大值是________.
题号:3832442
题型:填空题
难易度:一般
日期:2009-11-15
来源:2009高考真题汇编5-平面向量
【题文】已知向量

和向量
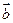
的夹角为

,
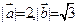
,则向量

和向量
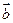
的数量积
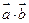
=
▲。
题号:1352389
题型:解答题
难易度:较易
日期:2010-02-13
来源:2009高考真题汇编5-平面向量
【题文】已知向量
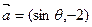
与
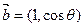
互相垂直,其中
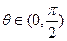
.
(1)求
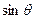
和
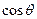
的值;(2)若
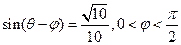
,求
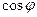
的值.
题号:1442794
题型:解答题
难易度:一般
日期:2009-11-25
来源:2009高考真题汇编5-平面向量
【题文】(本小题满分12分)
已知向量
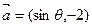
与
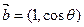
互相垂直,其中
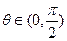
.
(1)求
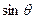
和
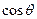
的值;
(2)若
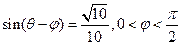
,求
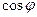
的值.
题号:1448526
题型:解答题
难易度:一般
日期:2009-11-15
来源:2009高考真题汇编5-平面向量
【题文】(本小题满分14分)设向量
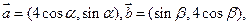

(1)若
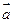
与
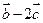
垂直,求

的值;(2)求
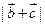
的最大值;
(3)若

,求证:
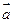
∥

. w.w.w.k.s.5.u.c.o.m

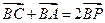 ,则( )
,则( )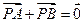
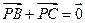
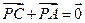
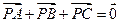
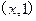 ,b=
,b=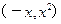 ,则向量
,则向量 ( )
( ) 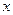 轴 B.平行于第一、三象限的角平分线
轴 B.平行于第一、三象限的角平分线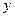 轴 D.平行于第二、四象限的角平分线
轴 D.平行于第二、四象限的角平分线  ,则它的边与半径为
,则它的边与半径为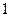 的圆的公共点个数最多为( )
的圆的公共点个数最多为( )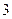
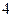


 ,
,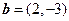 .若向量
.若向量 满足
满足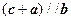 ,
,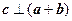 ,则
,则

 ( )
( )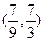

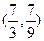


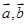 满足:
满足: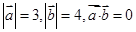 .以
.以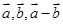 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为 的圆的公共点个数最多为 ( )
的圆的公共点个数最多为 ( )


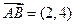 ,
,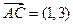 ,则
,则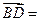 ( )
( )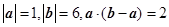 ,则向量
,则向量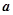 与向量
与向量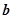 的夹角是( )
的夹角是( )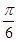

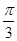

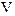 ABC所在平面内的一点,
ABC所在平面内的一点, ,则( )
,则( )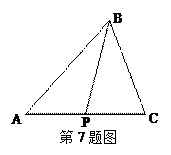
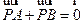
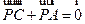

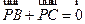
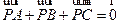

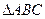 所在平面内,且
所在平面内,且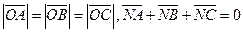 ,且
,且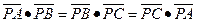 ,则点O,N,P依次是
,则点O,N,P依次是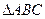 的( )
的( )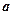 与
与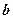 的夹角为
的夹角为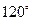 ,且
,且 ,那么
,那么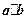 的值为 。
的值为 。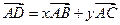 ,则
,则
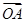 和
和 ,它们的夹角为
,它们的夹角为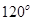 .如图所示,点C在以O为圆心的圆弧
.如图所示,点C在以O为圆心的圆弧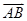 上变动.若
上变动.若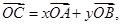 其中
其中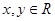 ,则
,则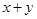 的最大值是________.
的最大值是________.
 和向量
和向量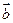 的夹角为
的夹角为 ,
,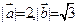 ,则向量
,则向量 和向量
和向量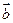 的数量积
的数量积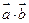 = ▲。
= ▲。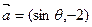 与
与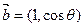 互相垂直,其中
互相垂直,其中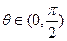 .
.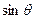 和
和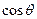 的值;(2)若
的值;(2)若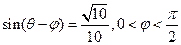 ,求
,求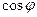 的值.
的值. 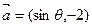 与
与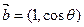 互相垂直,其中
互相垂直,其中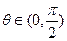 .
.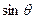 和
和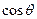 的值;
的值;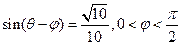 ,求
,求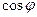 的值.
的值.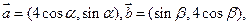
 (1)若
(1)若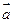 与
与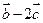 垂直,求
垂直,求 的值;(2)求
的值;(2)求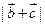 的最大值;
的最大值; ,求证:
,求证: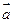 ∥
∥ . w.w.w.k.s.5.u.c.o.m
. w.w.w.k.s.5.u.c.o.m 