适用年级:{{getGradeNameByProperty('初三|中考模拟|广东|2015年')}} 试卷类型:{{getTestPaperTypeName('初三|中考模拟|广东|2015年')}} 使用省份:{{getAreaName('初三|中考模拟|广东|2015年')}}
试卷年份:{{getYear('初三|中考模拟|广东|2015年')}}上传日期:2015-09-11题数:25
提示:单击题文可显示答案与解析。
题号:587552
题型:选择题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
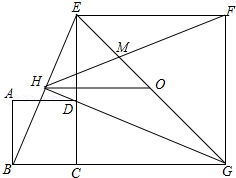
【题文】如图,正方形ABCD的边CD与正方形CEFG的边CE重合,点O是EG的中点,∠CGE的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:
①GH⊥BE;
②HO∥BG,HO=
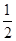
BG;
③点H不在正方形CGFE的外接圆上;
④△GBE∽△GMF.
其中结论正确的个数是( )
题号:587553
题型:选择题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为( )

A.60° B.45° C.30° D.15°
题号:587554
题型:选择题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】已知反比例函数
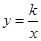
(k<0)的图象上两点A(x
1,y
1)、B(x
2,y
2),且x
1<x
2<0,则下列不等式恒成立的是( )
| A.y1•y2<0 | B.y1+y2<0 | C.y1-y2>0 | D.y1-y2<0 |
题号:587555
题型:选择题
难易度:较易
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】增城市4月份前5天的最高气温如下(单位:℃):27,30,24,30,31,对这组数据,下列说法正确的是( )
| A.平均数为28 | B.众数为30 | C.中位数为24 | D.方差为5 |
题号:587556
题型:选择题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】如图,PA、PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
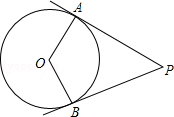
A.60° B.90° C.120° D.150
题号:587557
题型:选择题
难易度:较易
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】下列命题是假命题的是( )
| A.对角线互相平分的四边形是平行四边形 |
| B.对角线互相垂直的四边形是菱形 |
| C.对角线相等的平行四边形是矩形 |
| D.对角线相等的菱形是正方形 |
题号:587558
题型:选择题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
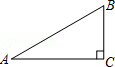
【题文】如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( )
题号:587559
题型:选择题
难易度:较易
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】计算:
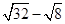
的结果是( )
题号:587560
题型:选择题
难易度:较易
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
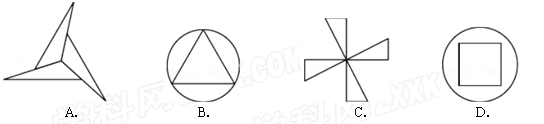
【题文】下列图形中,既是轴对称图形又是中心对称图形的是( )
题号:587561
题型:选择题
难易度:容易
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】
| A.2 | B. | C.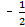 | D.-2 |
题号:587546
题型:填空题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】一个几何体的三视图如图,根据图示的数据计算该几何体的表面积是
.(结果保留π).
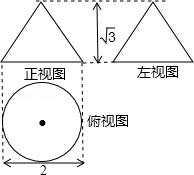
题号:587547
题型:填空题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】若α,β是一元二次方程x2-x-1=0的两个实数根,则α2+αβ+β2的值为 .
题号:587548
题型:填空题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】在二次函数y=-2(x-3)2+1中,若y随x的增大而增大,则x的取值范围是 .
题号:587550
题型:填空题
难易度:较易
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】代数式
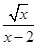
有意义时,x应满足的条件为
.
题号:587551
题型:填空题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】正多边形一个外角的度数是60°,则该正多边形的边数是 .
题号:4874077
题型:填空题
难易度:容易
日期:2017-09-01
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】若点P在线段AB的垂直平分线上,PA=5,则PB=______.
题号:587538
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】如图①,在Rt△ABC和Rt△EDC中,∠ACB=∠ECD=90°,AC=EC=BC=DC,AB与EC交于F,ED与AB、BC分别交于M、H.
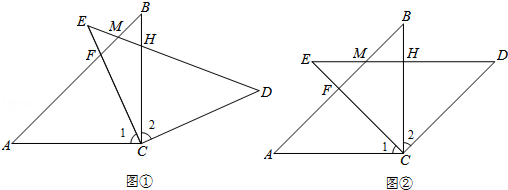
(1)求证:CF=CH;
(2)如图②,Rt△ABC不动,将Rt△EDC绕点C旋转到∠BCE=45°时,判断四边形ACDM的形状,并证明你的结论.
题号:587539
题型:解答题
难易度:较难
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】如图,抛物线y=-x
2+bx+c的顶点为D,与x轴交于A(-1,0)、B(3,0),与y轴交于点C.

(1)求该抛物线的解析式;
(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当四边形OBMC的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当四边形OBMC的面积最大时,在抛物线的对称轴上是否存在点Q,使得△CNQ为直角三角形?若存在,直接写出点Q的坐标.
题号:587540
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
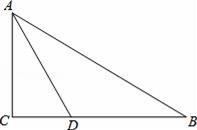
(1)动手操作:利用尺规作⊙O,使⊙O经过点A、D,且圆心O在AB上;并标出⊙O与AB的另一个交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①判断直线BC与⊙O的位置关系,并说明理由;
②若AB=6,BD=2
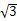
,求线段BD、BE与劣弧
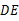
所围成的图形面积(结果保留根号和π).
题号:587541
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】为了顺利通过“国家文明城市”验收,市政府拟对部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完成工程,又能使工程费用最少?
题号:587542
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=-
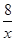
的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
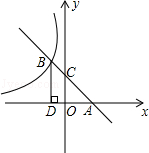
(1)求直线AB的解析式;
(2)若点P是线段BD上一点,且△PBC的面积等于3,求点P的坐标.
题号:587543
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
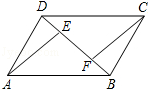
【题文】如图,AB为⊙O的直径,劣弧
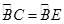
,BD∥CE,连接AE并延长交BD于D.求证:
(1)AC=AE;
(2)AB
2=AC•AD.
题号:587544
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
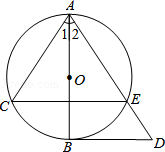
【题文】如图,在▱ABCD中,BE=DF.求证:AE=CF.
题号:587545
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】计算:(x-3)2-(1-x)•(3-x)-2.
题号:3462631
题型:解答题
难易度:一般
日期:2015-09-11
来源:2015届广东省广州市增城市初中毕业班综合测试数学试卷(带解析)
【题文】为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
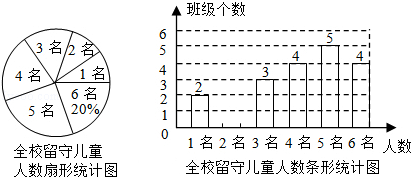
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
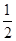 BG;
BG;

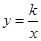 (k<0)的图象上两点A(x1,y1)、B(x2,y2),且x1<x2<0,则下列不等式恒成立的是( )
(k<0)的图象上两点A(x1,y1)、B(x2,y2),且x1<x2<0,则下列不等式恒成立的是( )

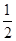
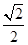
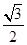
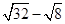 的结果是( )
的结果是( )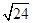
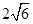
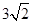
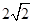


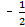

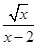 有意义时,x应满足的条件为 .
有意义时,x应满足的条件为 .


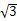 ,求线段BD、BE与劣弧
,求线段BD、BE与劣弧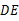 所围成的图形面积(结果保留根号和π).
所围成的图形面积(结果保留根号和π).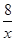 的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
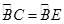 ,BD∥CE,连接AE并延长交BD于D.求证:
,BD∥CE,连接AE并延长交BD于D.求证:

