适用年级:{{getGradeNameByProperty('高三|高考真卷|湖北|2011年')}} 试卷类型:{{getTestPaperTypeName('高三|高考真卷|湖北|2011年')}} 使用省份:{{getAreaName('高三|高考真卷|湖北|2011年')}}
试卷年份:{{getYear('高三|高考真卷|湖北|2011年')}}上传日期:2014-06-05题数:21
提示:单击题文可显示答案与解析。
题号:913705
题型:选择题
难易度:一般
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
题号:913706
题型:选择题
难易度:一般
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)直线2x+y﹣10=0与不等式组

表示的平面区域的公共点有( )
题号:913707
题型:选择题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)设球的体积为V
1,它的内接正方体的体积为V
2,下列说法中最合适的是( )
| A.V1比V2大约多一半 | B.V1比V2大约多两倍半 |
| C.V1比V2大约多一倍 | D.V1比V2大约多一倍半 |
题号:913708
题型:选择题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
题号:913709
题型:选择题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)将两个顶点在抛物线y
2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则( )
题号:913710
题型:选择题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=e
x,则g(x)=( )
| A.ex﹣e﹣x | B. (ex+e﹣x) (ex+e﹣x) | C. (e﹣x﹣ex) (e﹣x﹣ex) | D. (ex﹣e﹣x) (ex﹣e﹣x) |
题号:913711
题型:选择题
难易度:一般
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)若向量

=(1,2),
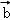
=(1,﹣1),则2
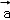
+
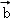
与
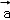
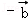
的夹角等于( )
题号:913721
题型:选择题
难易度:容易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)已知U={1,2,3,4,5,6,7,8},A={1,3,5,7},B={2,4,5}则∁U(A∪B)( )
A.{6,8} B.{5,7} C.{4,6,7} D.{1,3,5,6,8}
题号:3759158
题型:选择题
难易度:容易
日期:2014-06-06
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
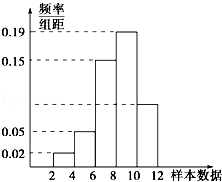
【题文】(5分)(2011•湖北)有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
题号:3759159
题型:选择题
难易度:一般
日期:2014-06-06
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)若实数a,b满足a≥0,b≥0,且ab=0,则称a与b互补,记φ(a,b)=
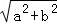
﹣a﹣b那么φ(a,b)=0是a与b互补的( )
| A.必要不充分条件 | B.充分不必要的条件 |
| C.充要条件 | D.既不充分也不必要条件 |
题号:913701
题型:填空题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)过点(﹣1,2)的直线l被圆x
2+y
2﹣2x﹣2y+1=0截得的弦长
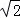
,则直线l的斜率为
.
题号:913702
题型:填空题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到一瓶已过保质期的概率为 .(结果用最简分数表示)
题号:913703
题型:填空题
难易度:一般
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)(x﹣
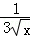
)
18的展开式中含x
15的项的系数为
.(结果用数值表示)
题号:913704
题型:填空题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)某市有大型超市200家、中型超市400家、小型超市1400家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市 家.
题号:3759160
题型:填空题
难易度:较易
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(5分)(2011•湖北)里氏震级M的计算公式为:M=lgA﹣lgA0,其中A是测震仪记录的地震曲线的最大振幅,是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅A0为0.001,则此次地震的震级为 级;9级地震的最大的振幅是5级地震最大振幅的 倍.
题号:913696
题型:解答题
难易度:较难
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(14分)(2011•湖北)平面内与两定点A1(﹣a,0),A2(a,0)(a>0)连线的斜率之积等于非零常数m的点的轨迹,加上A1、A2两点所成的曲线C可以是圆、椭圆成双曲线.
(Ⅰ)求曲线C的方程,并讨论C的形状与m值的关系;
(Ⅱ)当m=﹣1时,对应的曲线为C1;对给定的m∈(﹣1,0)∪(0,+∞),对应的曲线为C2,设F1、F2是C2的两个焦点.试问:在C1上,是否存在点N,使得△F1NF2的面积S=|m|a2.若存在,求tanF1NF2的值;若不存在,请说明理由.
题号:913697
题型:解答题
难易度:较难
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(13分)(2011•湖北)设函数f(x)=x3+2ax2+bx+a,g(x)=x2﹣3x+2,其中x∈R,a、b为常数,已知曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l.
(Ⅰ) 求a、b的值,并写出切线l的方程;
(Ⅱ)若方程f(x)+g(x)=mx有三个互不相同的实根0、x1、x2,其中x1<x2,且对任意的x∈[x1,x2],f(x)+g(x)<m(x﹣1)恒成立,求实数m的取值范围.
题号:913698
题型:解答题
难易度:较难
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(12分)(2011•湖北)如图,已知正三棱柱ABC﹣A
1B
1C
1的底面边长为2,侧棱长为3
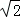
,点E在侧棱AA
1上,点F在侧棱BB
1上,且AE=2
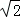
,BF=
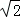
.
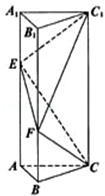
(I) 求证:CF⊥C
1E;
(II) 求二面角E﹣CF﹣C
1的大小.
题号:913699
题型:解答题
难易度:较难
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(12分)(2011•湖北)成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{b
n}中的b
3、b
4、b
5.
(Ⅰ)求数列{b
n}的通项公式;
(Ⅱ)数列{b
n}的前n项和为S
n,求证:数列{S
n+
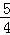
}是等比数列.
题号:913700
题型:解答题
难易度:一般
日期:2014-06-05
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(12分)(2011•湖北)设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=

(Ⅰ)求△ABC的周长;
(Ⅱ)求cos(A﹣C)的值.
题号:3759161
题型:解答题
难易度:一般
日期:2014-06-06
来源:2011年普通高等学校招生全国统一考试文科数学(湖北卷带解析)
【题文】(12分)(2011•湖北)提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(Ⅰ)当0≤x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x•v(x)可以达到最大,并求出最大值.(精确到1辆/小时).
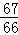 升
升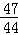 升
升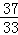 升
升 表示的平面区域的公共点有( )
表示的平面区域的公共点有( )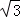 sinx﹣cosx,x∈R,若f(x)≥1,则x的取值范围为( )
sinx﹣cosx,x∈R,若f(x)≥1,则x的取值范围为( )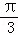 ≤x≤kπ+π,k∈Z}
≤x≤kπ+π,k∈Z}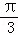 ≤x≤2kπ+π,k∈Z}
≤x≤2kπ+π,k∈Z}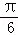 ≤x≤kπ+
≤x≤kπ+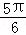 ,k∈Z}
,k∈Z}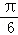 ≤x≤2kπ+
≤x≤2kπ+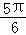 ,k∈Z}
,k∈Z} (ex+e﹣x)
(ex+e﹣x) (e﹣x﹣ex)
(e﹣x﹣ex) (ex﹣e﹣x)
(ex﹣e﹣x) =(1,2),
=(1,2),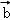 =(1,﹣1),则2
=(1,﹣1),则2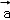 +
+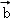 与
与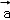
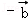 的夹角等于( )
的夹角等于( )
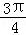

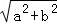 ﹣a﹣b那么φ(a,b)=0是a与b互补的( )
﹣a﹣b那么φ(a,b)=0是a与b互补的( )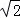 ,则直线l的斜率为 .
,则直线l的斜率为 .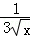 )18的展开式中含x15的项的系数为 .(结果用数值表示)
)18的展开式中含x15的项的系数为 .(结果用数值表示)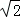 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2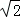 ,BF=
,BF=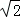 .
.
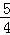 }是等比数列.
}是等比数列.