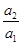 ,
,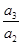 ,…,
,…,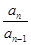 ,…是首项为1,公比为-
,…是首项为1,公比为-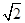 的等比数列,那么a5等于( )
的等比数列,那么a5等于( )| A.32 | B.64 |
| C.-32 | D.-64 |
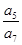 等于( )
等于( )A.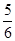 | B.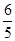 | C.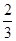 | D.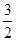 |
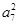 =4π,则tan(a2a12)的值为( )
=4π,则tan(a2a12)的值为( )A.±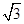 | B.-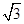 | C.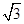 | D.-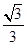 |
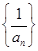 的前5项和为( )
的前5项和为( )A.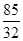 | B.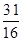 | C.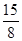 | D.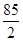 |
| A.(n+1)2 | B.n2 |
| C.n(2n-1) | D.(n-1)2 |
| A.1 | B.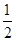 | C.-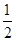 | D.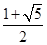 |
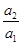 等于( )
等于( )| A.1 | B.2 | C.3 | D.4 |
A.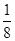 | B.-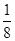 | C.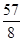 | D.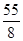 |
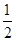 ,a3=
,a3=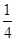 ,ak=
,ak=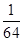 ,则k等于( )
,则k等于( )| A.5 | B.6 | C.7 | D.8 |
A.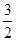 | B.2 | C.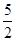 | D.3 |
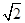 -1,a5=
-1,a5=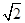 +1,则
+1,则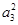 +2a2a6+a3a7等于( )
+2a2a6+a3a7等于( )| A.4 | B.6 | C.8 | D.8-4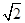 |
A.5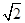 | B.7 | C.6 | D.4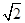 |
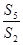 等于( )
等于( )| A.-11 | B.-8 | C.5 | D.11 |
| A.3 | B.4 | C.5 | D.6 |
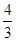 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )| A.-6(1-3-10) | B.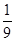 (1-310) (1-310) |
| C.3(1-3-10) | D.3(1+3-10) |
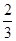 的等比数列{an}的前n项和为Sn,则( )
的等比数列{an}的前n项和为Sn,则( )| A.Sn=2an-1 | B.Sn=3an-2 |
| C.Sn=4-3an | D.Sn=3-2an |
| A.(-2)n-1 | B.-(-2)n-1 |
| C.(-2)n | D.-(-2)n |
| A.2 | B.4 | C.8 | D.16 |
| A.1 | B.2 | C.4 | D.8 |
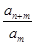 =an,则a3= ;{an}的前n项和Sn= .
=an,则a3= ;{an}的前n项和Sn= . 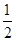 ,a4=4,则公比q= ;a1+a2+…+an= .
,a4=4,则公比q= ;a1+a2+…+an= . 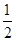 ,则a1
,则a1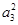 a5= .
a5= . 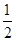 ,an,Sn成等差数列.
,an,Sn成等差数列.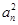 =
=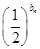 ,设cn=
,设cn=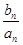 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.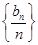 为等比数列,并求数列{bn}的通项公式.
为等比数列,并求数列{bn}的通项公式.| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |