适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-22题数:6
提示:单击题文可显示答案与解析。
题号:743521
题型:解答题
难易度:一般
日期:2016-05-31
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(带解析)
【题文】在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA ⊥面ABCD.
(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD 的体积取到最大值,
①求此时PA的长度;
②求此时二面角A-DE-B的余弦值的大小.
题号:947601
题型:解答题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(带解析)
【题文】如图,
AB是圆的直径,
PA垂直圆所在的平面,
C是圆上的点.
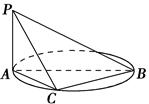
(1)求证:平面
PAC⊥平面
PBC;
(2)若
AB=2,
AC=1,
PA=1,求二面角
C
PB
A的余弦值..
题号:947603
题型:解答题
难易度:困难
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(带解析)
【题文】如图,在直三棱柱
ABC-
A1B1C1中,
D,
E分别是
AB,
BB1的中点,
AA1=
AC=
CB=
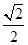 AB
AB.
(1)证明:
BC1∥平面
A1CD;
(2)求二面角
D-
A1C-
E的正弦值.
题号:3917448
题型:解答题
难易度:一般
日期:2017-07-24
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(带解析)
【题文】如图,在四棱锥
P-
ABCD中,
PC⊥底面
ABCD,底面
ABCD是直角梯形,
AB⊥
AD,
AB∥
CD,
AB=2
AD=2
CD=2,
E是
PB的中点.
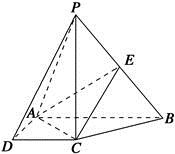
(1)求证:平面
EAC⊥平面
PBC;
(2)若二面角
P-
AC-
E的余弦值为
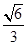
,求直线
PA与平面
EAC所成角的正弦值.
题号:4187616
题型:解答题
难易度:一般
日期:2014-03-23
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(带解析)
【题文】如图,四棱柱
ABCD-
A1B1C1D1的底面
ABCD是正方形,
O为底面中心,
A1O⊥平面
ABCD,
AB=
AA1=
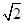
.
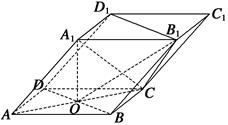
(1)证明:
A1C⊥平面
BB1D1D;
(2)求平面
OCB1与平面
BB1D1D的夹角
θ的大小.
题号:4187617
题型:解答题
难易度:一般
日期:2014-03-23
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(带解析)
【题文】如图,四棱柱
ABCD-
A1B1C1D1中,侧棱
A1A⊥底面
ABCD,
AB∥
DC,
AB⊥
AD,
AD=
CD=1,
AA1=
AB=2,
E为棱
AA1的中点.
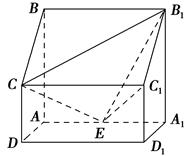
(1)证明
B1C1⊥
CE;
(2)求二面角
B1-
CE-
C1的正弦值;
(3)设点
M在线段
C1E上,且直线
AM与平面
ADD1A1所成角的正弦值为
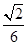
,求线段
AM的长.

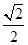 AB.
AB.

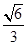 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.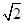 .
.

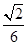 ,求线段AM的长.
,求线段AM的长.