适用年级:{{getGradeNameByProperty('高三|高考模拟|北京|2011年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|北京|2011年')}} 使用省份:{{getAreaName('高三|高考模拟|北京|2011年')}}
试卷年份:{{getYear('高三|高考模拟|北京|2011年')}}上传日期:2011-04-07题数:20
提示:单击题文可显示答案与解析。
题号:1163495
题型:选择题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】定义区间
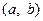
,
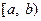
,
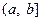
,
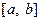
的长度均为
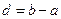
,多个区间并集的长度为各区间长度之和,例如,
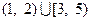
的长度
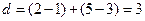
. 用
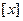
表示不超过
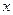
的最大整数,记
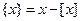
,其中
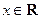
. 设
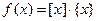
,
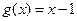
,若用
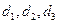
分别表示不等式
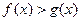
,方程
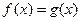
,不等式
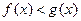
解集区间的长度,则当
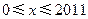
时,有
题号:1163496
题型:选择题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】如图,双曲线的中心在坐标原点
,
分别是双曲线虚轴的上、下顶点,
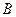
是双曲线的左顶点,
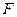
为双曲线的左焦点,直线
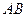
与
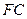
相交于点
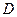
.若双曲线的离心率为2,则
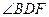
的余弦值是
题号:1163497
题型:选择题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】函数
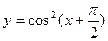
的单调增区间是
题号:1163498
题型:选择题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】已知

是由正数组成的等比数列,

表示

的前

项的和.若

,

,则

的值是()
题号:1163499
题型:选择题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】极坐标方程
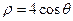
化为直角坐标方程是
题号:1163500
题型:选择题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从两个班抽出16人参加军训表演,则一班和二班分别被抽取的人数是
| A.8,8 | B. 10,6 10,6 | C.9,7 | D.12,4 |
题号:1163501
题型:选择题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
题号:3476798
题型:选择题
难易度:较易
日期:2013-03-14
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】.已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于

题号:1163490
题型:填空题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】.对于各数互不相等的整数数组
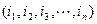
(
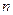
是不小于3的正整数),对于任意的
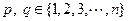
,当
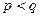
时有
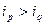
,则称
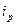
,
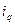
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称

为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于 ;若数组
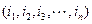
中的逆序数为
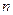
,则数组
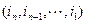
中的逆序数为 .
题号:1163491
题型:填空题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
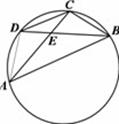
【题文】如下图,在圆内接四边形
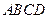
中, 对角线
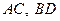
相交于点
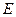
.已
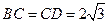
,
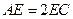
,
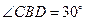
,则
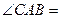
,
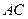
的长是

.
题号:1163492
题型:填空题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
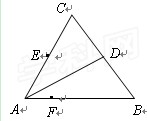
【题文】如图,

在三角形
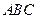
中,
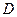
,
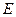
分别为
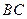
,
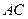
的中点,
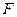
为
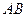
上的点,且
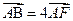
. 若
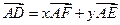
,则实数
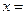
,实数
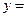
.
题号:1163493
题型:填空题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】在二项式
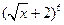
的展开式中,第四项的系数是 .
题号:1163494
题型:填空题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
题号:3476799
题型:填空题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】执行下图所示的程序框图,若输入
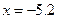
,则输出
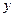
的值为 .
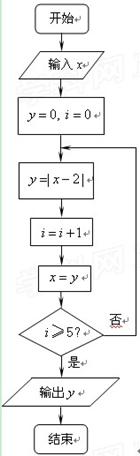
题号:1163487
题型:解答题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】(本小题满分14分)
有
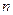
个首项都是1的等差数列,设第
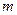
个数列的第
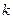
项为
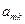
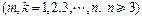
,公差为
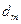

,并且
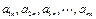
成等差数列.
(Ⅰ)证明
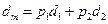
(
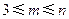
,
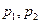
是

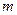
的多项式),并求
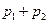
的值
(Ⅱ)当
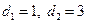
时,将数列
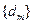
分组如下:
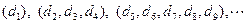
(每组数的个数构成

等差数列).
设前
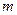
组中所有数之和为
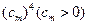
,求数列
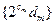
的前
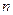
项和
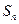
.
(Ⅲ)设
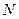
是不超过20的正整数,当
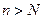
时,对于(Ⅱ)中的
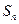
,求使得不等式
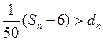
成立的所有
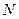
的值.
题号:1163488
题型:解答题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】(本小题满分14分)
已知
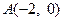
,
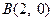
为椭圆
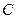
的左、右顶点,
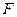
为其右焦点,
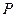
是椭圆
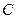
上异于
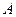
,
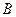
的动点,且
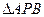
面积的最大值为
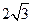
.
(Ⅰ)求椭圆
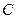
的方程及离心率;
(Ⅱ)直线
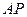
与椭圆在点
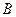
处的切线交于点
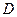
,当直线
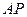
绕点
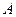
转动时,试判断以
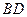

为直径的圆与直线
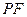
的位置关系,并加以证明.
题号:1163489
题型:解答题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】
(本小题满分13分)
在锐角
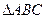
中,角
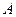
,
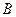
,
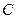
所对的边分别为
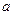
,
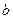
,
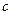
.已知
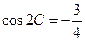
.
(Ⅰ)求
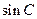
;
(Ⅱ)当
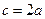
,且
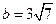
时,求
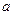
.
题号:3476800
题型:解答题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】(本小题满分13分)
如图,在四棱锥
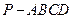
中,底面
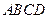
为直角

梯形,且
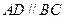
,
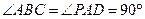
,侧面
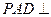
底面
. 若
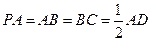
.
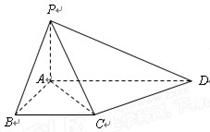
(Ⅰ)求证:
平面
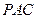
;
(Ⅱ)侧棱
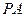
上是否存在点
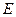
,使得
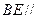
平面
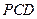
?若存在,指出点
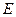
的位置并证明,若不存在,请说明理由;
(Ⅲ)求二面角
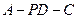
的余弦值.
题号:3476801
题型:解答题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】(本小题满分13分)
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是
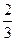
.
(

Ⅰ)记教师甲在每场

的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比

赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
题号:3476802
题型:解答题
难易度:较易
日期:2011-04-07
来源:2011届北京市朝阳区高三第一次综合练习数学理卷
【题文】(本小题满分13分)
已知函数
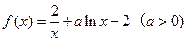
.
(Ⅰ)若曲线
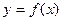
在点
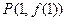
处的切线与直线
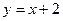
垂直,求函数
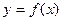
的单调区间;
(Ⅱ)若对于
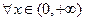
都有
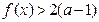
成立,试求
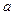
的取值范围;
(Ⅲ)记
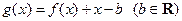
.当
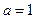
时,函数
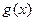
在区间
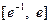
上有两个零点,求实数
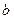
的取值范围.
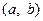 ,
,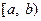 ,
,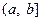 ,
,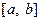 的长度均为
的长度均为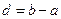 ,多个区间并集的长度为各区间长度之和,例如,
,多个区间并集的长度为各区间长度之和,例如, 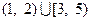 的长度
的长度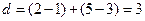 . 用
. 用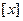 表示不超过
表示不超过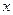 的最大整数,记
的最大整数,记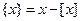 ,其中
,其中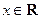 . 设
. 设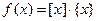 ,
,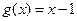 ,若用
,若用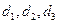 分别表示不等式
分别表示不等式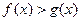 ,方程
,方程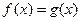 ,不等式
,不等式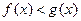 解集区间的长度,则当
解集区间的长度,则当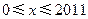 时,有
时,有 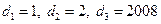
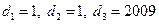
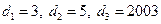
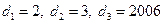
 ,
,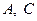 分别是双曲线虚轴的上、下顶点,
分别是双曲线虚轴的上、下顶点,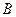 是双曲线的左顶点,
是双曲线的左顶点,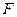 为双曲线的左焦点,直线
为双曲线的左焦点,直线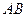 与
与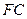 相交于点
相交于点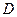 .若双曲线的离心率为2,则
.若双曲线的离心率为2,则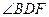 的余弦值是
的余弦值是 
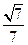
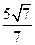
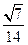
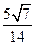
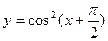 的单调增区间是
的单调增区间是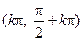
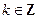
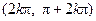
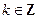
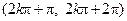
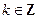
 是由正数组成的等比数列,
是由正数组成的等比数列, 表示
表示 的前
的前 项的和.若
项的和.若 ,
, ,则
,则 的值是()
的值是()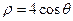 化为直角坐标方程是
化为直角坐标方程是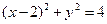
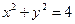
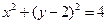
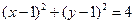
 10,6
10,6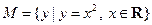 ,
,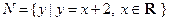 ,则
,则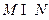 等于
等于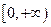
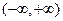
 {
{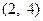 ,
,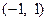 }
}
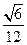
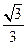
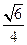
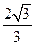
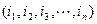 (
(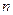 是不小于3的正整数),对于任意的
是不小于3的正整数),对于任意的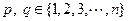 ,当
,当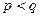 时有
时有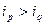 ,则称
,则称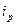 ,
,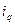 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称 为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于 ;若数组
为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于 ;若数组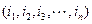 中的逆序数为
中的逆序数为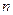 ,则数组
,则数组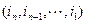 中的逆序数为 .
中的逆序数为 .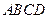 中, 对角线
中, 对角线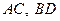 相交于点
相交于点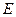 .已
.已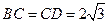 ,
,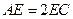 ,
,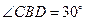 ,则
,则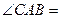 ,
,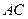 的长是
的长是  .
.
 在三角形
在三角形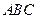 中,
中,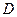 ,
,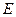 分别为
分别为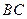 ,
,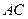 的中点,
的中点,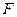 为
为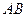 上的点,且
上的点,且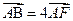 . 若
. 若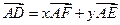 ,则实数
,则实数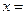 ,实数
,实数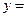 .
.
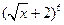 的展开式中,第四项的系数是 .
的展开式中,第四项的系数是 .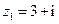 ,
,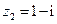 ,则
,则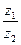 等于 .
等于 .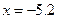 ,则输出
,则输出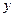 的值为 .
的值为 .
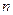 个首项都是1的等差数列,设第
个首项都是1的等差数列,设第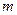 个数列的第
个数列的第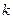 项为
项为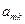
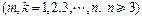 ,公差为
,公差为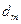
 ,并且
,并且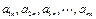 成等差数列.
成等差数列.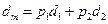 (
(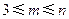 ,
,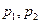 是
是
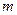 的多项式),并求
的多项式),并求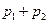 的值
的值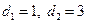 时,将数列
时,将数列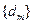 分组如下:
分组如下: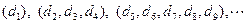 (每组数的个数构成
(每组数的个数构成 等差数列).
等差数列).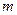 组中所有数之和为
组中所有数之和为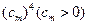 ,求数列
,求数列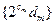 的前
的前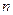 项和
项和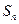 .
.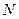 是不超过20的正整数,当
是不超过20的正整数,当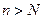 时,对于(Ⅱ)中的
时,对于(Ⅱ)中的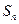 ,求使得不等式
,求使得不等式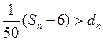 成立的所有
成立的所有 的值.
的值.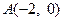 ,
,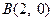 为椭圆
为椭圆 的左、右顶点,
的左、右顶点,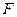 为其右焦点,
为其右焦点,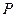 是椭圆
是椭圆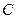 上异于
上异于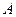 ,
,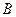 的动点,且
的动点,且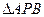 面积的最大值为
面积的最大值为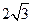 .
. 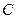 的方程及离心率;
的方程及离心率;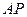 与椭圆在点
与椭圆在点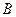 处的切线交于点
处的切线交于点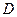 ,当直线
,当直线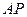 绕点
绕点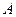 转动时,试判断以
转动时,试判断以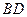

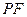 的位置关系,并加以证明.
的位置关系,并加以证明.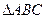 中,角
中,角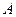 ,
,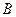 ,
,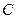 所对的边分别为
所对的边分别为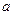 ,
,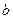 ,
,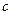 .已知
.已知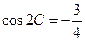 .
.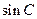 ;
;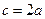 ,且
,且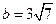 时,求
时,求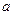 .
.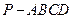 中,底面
中,底面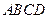 为直角
为直角 梯形,且
梯形,且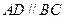 ,
,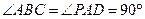 ,侧面
,侧面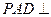 底面
底面 . 若
. 若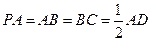 .
.
 平面
平面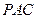 ;
;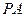 上是否存在点
上是否存在点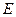 ,使得
,使得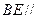 平面
平面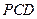 ?若存在,指出点
?若存在,指出点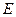 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;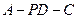 的余弦值.
的余弦值.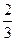 .
. Ⅰ)记教师甲在每场
Ⅰ)记教师甲在每场 的6次投球中投进球的个数为X,求X的分布列及数学期望;
的6次投球中投进球的个数为X,求X的分布列及数学期望; 赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗? 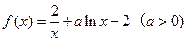 .
.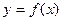 在点
在点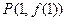 处的切线与直线
处的切线与直线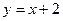 垂直,求函数
垂直,求函数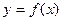 的单调区间;
的单调区间;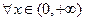 都有
都有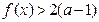 成立,试求
成立,试求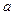 的取值范围;
的取值范围;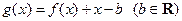 .当
.当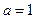 时,函数
时,函数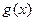 在区间
在区间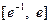 上有两个零点,求实数
上有两个零点,求实数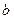 的取值范围.
的取值范围.