适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2010年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2010年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2010年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2010年')}}上传日期:2010-06-25题数:19
提示:单击题文可显示答案与解析。
题号:156215
题型:选择题
难易度:一般
日期:2015-01-16
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有
题号:1258290
题型:选择题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
题号:1261489
题型:选择题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有
| A. 504种 | B. 960种 | C. 1008种 | D. 1108种 |
题号:1261830
题型:选择题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】

展开式中不含

项的系数的和为
题号:3411191
题型:选择题
难易度:较难
日期:2012-05-29
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】某校开设
A类选修课3门,
B类选修课4门,一位同学从中共选3门.若要求两类课程中各至少选一门,则不同的选法共有
题号:3603245
题型:选择题
难易度:一般
日期:2013-04-09
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是
(A)72 (B)96 (C) 108 (D)144
题号:3606854
题型:选择题
难易度:较易
日期:2012-07-02
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】
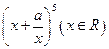
展开式中
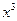
的系数为10,则实数a等于【】
| A.-1 | B.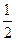 | C.1 | D.2 |
题号:3606855
题型:选择题
难易度:较易
日期:2012-09-12
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为
题号:3606856
题型:选择题
难易度:较易
日期:2013-03-21
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有
题号:3606857
题型:选择题
难易度:较难
日期:2010-06-11
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为
题号:3606858
题型:选择题
难易度:一般
日期:2013-07-22
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
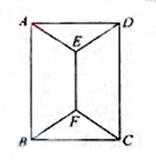
【题文】如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
题号:3606860
题型:选择题
难易度:一般
日期:2012-07-12
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】现安排甲、乙、丙、丁、戌5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加。甲、乙不会开车但能从事其他三项工作,丙丁戌都能胜任四项工作,则不同安排方案的种数是
题号:1260971
题型:填空题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】在(x+
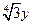
)
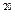
的展开式中,系数为有理数的项共有_______项。
题号:1261162
题型:填空题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
题号:1262424
题型:填空题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】
有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、
“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复. 若上午不测“握
力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人. 则不同的安排方式共
有______________种(用数字作答).
题号:1262440
题型:填空题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】
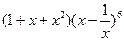
的展开式中的常数项为_________.
题号:3603249
题型:填空题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】
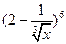
的展开式中的第四项是
. w_w_w.k*s 5*u.c o*m
题号:3606853
题型:填空题
难易度:较难
日期:2010-06-08
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】
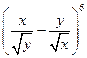
展开式中,
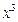
的系数等于________。
题号:3606859
题型:填空题
难易度:一般
日期:2013-04-09
来源:2010年高考试题分项版理科数学之专题十 排列、组合、二项式定理
【题文】
将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有 种(用数字作答).
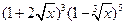 的展开式中x的系数是
的展开式中x的系数是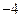
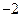
 展开式中不含
展开式中不含 项的系数的和为
项的系数的和为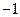
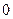

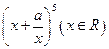 展开式中
展开式中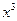 的系数为10,则实数a等于【】
的系数为10,则实数a等于【】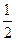

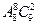

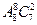

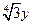 )
)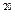 的展开式中,系数为有理数的项共有_______项。
的展开式中,系数为有理数的项共有_______项。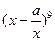 的展开式中
的展开式中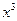 的系数是
的系数是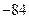 ,则
,则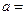 .
.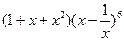 的展开式中的常数项为_________.
的展开式中的常数项为_________.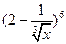 的展开式中的第四项是 . w_w_w.k*s 5*u.c o*m
的展开式中的第四项是 . w_w_w.k*s 5*u.c o*m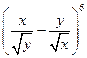 展开式中,
展开式中,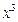 的系数等于________。
的系数等于________。