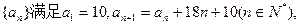 记
记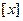 表示不超过实数x的最大整数,令
表示不超过实数x的最大整数,令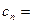
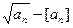 ,当
,当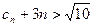 时,
时,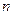 的最小值是
的最小值是| A.2 | B.1 | C.3 | D.4 |
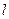 是双曲线
是双曲线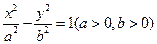 的右准线,以原点O为圆心且过双曲线焦点的圆被直线
的右准线,以原点O为圆心且过双曲线焦点的圆被直线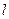 分成弧长为2:1的两段,则双曲线的离心率为
分成弧长为2:1的两段,则双曲线的离心率为A.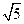 | B.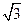 | C.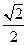 | D.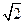 |
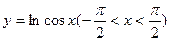 的图像大致是
的图像大致是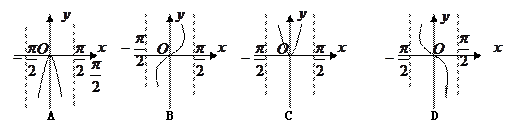
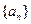 中,
中,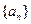 不恒为零,若
不恒为零,若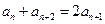 ,且
,且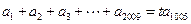 ,则
,则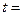
| A.2007 | B.2008 | C.2009 | D.2010 |
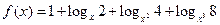 ,则使
,则使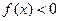 的
的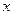 的取值范围是
的取值范围是 A.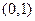 | B.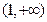 | C.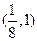 | D.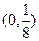 |
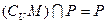 ,则
,则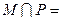
| A.M | B.P | C.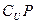 | D.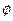 |
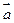 、
、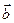 是不共线的向量,
是不共线的向量,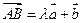 ,
,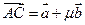
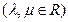 ,则
,则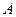 、
、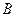 、
、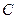 三点共线的充要条件是
三点共线的充要条件是A.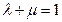 | B.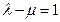 | C.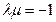 | D.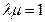 |
A.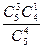 | B.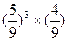 | C.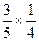 | D.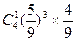 |
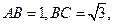 A、C两点间的球面距离为
A、C两点间的球面距离为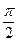 ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为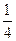 B.
B. 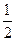 C.
C. 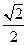 D.
D. 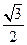
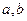 是实数,则“
是实数,则“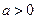 且
且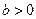 ”是“
”是“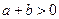 且
且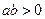 ”的
”的 | A.充分而不必要条件 | B.必要而不充分条件. |
| C.充分必要条件 | D.既不充分也不必要条件 |
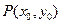 到直线
到直线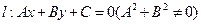 的有向距离为
的有向距离为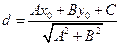 .已知点
.已知点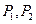 到直线
到直线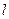 的有向距离分别是
的有向距离分别是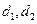 ,给出以下命题:
,给出以下命题: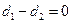 ,则直线
,则直线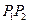 与直线
与直线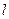 平行;②若
平行;②若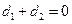 ,则直线
,则直线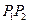 与直线
与直线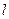 平行;
平行;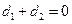 ,则直线
,则直线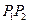 与直线
与直线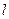 垂直;④若
垂直;④若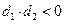 ,则直线
,则直线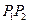 与直线
与直线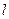 相交;其中正确命题的序号是 .
相交;其中正确命题的序号是 .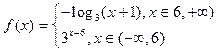 的反函数为
的反函数为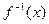 ,若
,若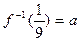 ,则
,则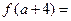 .
.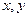 满足条件
满足条件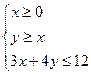 ,则
,则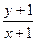 的最大值为 .
的最大值为 .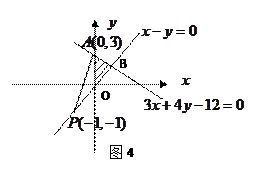
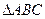 中,
中,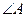 ,
,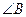 ,
,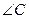 所对的边分别是
所对的边分别是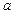 ,
,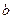 ,
,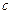 ,已知
,已知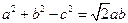 ,则
,则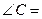 .
.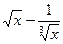 )10的常数项是 (用数字作答).
)10的常数项是 (用数字作答).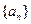 中,
中,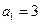 ,
,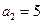 ,其前
,其前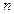 项和
项和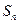 满足
满足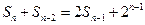
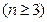 ,令
,令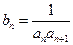 .
.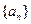 的通项公式;
的通项公式;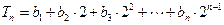 ,求证:
,求证: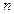 ,都有
,都有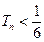 ;
; 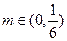 ,均存在
,均存在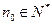 ,使得
,使得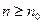 时,
时,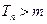 .
.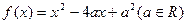 .
.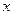 的不等式
的不等式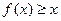 的解集为R,求
的解集为R,求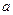 的取值范围;
的取值范围;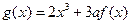 ,若
,若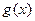 在区间
在区间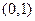 上存在极小值,求实数
上存在极小值,求实数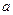 的取值范围.
的取值范围.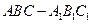 的各棱长都为
的各棱长都为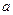 ,
,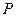 为棱
为棱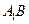 上的动点.
上的动点.
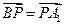 时,求证:
时,求证: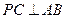 ;
; 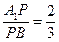 ,求二面角
,求二面角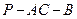 的大小;
的大小; 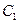 到平面
到平面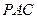 的距离.
的距离.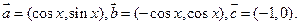
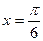 时,求向量
时,求向量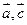 的夹角
的夹角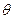 ;
; 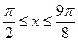 时,求函数
时,求函数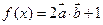 的最大值.
的最大值.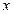 轴上动点
轴上动点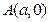 引抛物线
引抛物线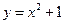 的两条切线
的两条切线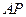 、
、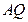 ,
,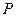 、
、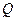 为切点.
为切点.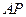 ,
,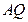 的斜率分别为
的斜率分别为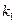 和
和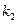 ,求证:
,求证: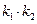 为定值,并求出定值;
为定值,并求出定值; (Ⅱ)求证:直线
(Ⅱ)求证:直线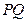 恒过定点,并求出定点坐标;
恒过定点,并求出定点坐标; 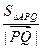 最小时,求
最小时,求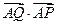 的值.
的值.