适用年级:{{getGradeNameByProperty('高三|高考模拟|河北|2017年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|河北|2017年')}} 使用省份:{{getAreaName('高三|高考模拟|河北|2017年')}}
试卷年份:{{getYear('高三|高考模拟|河北|2017年')}}上传日期:2017-03-15题数:23
提示:单击题文可显示答案与解析。
题号:3419574
题型:选择题
难易度:困难
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】已知双曲线
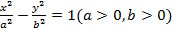
的左右焦点分别为
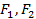
,过点
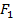
且垂直于
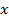
轴的直线与该双曲线的左支交于
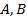
两点,
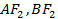
分别交
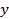
轴于
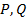
两点,若
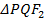
的周长为12,则
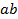
取得最大值时该双曲线的离心率为( )
题号:3419575
题型:选择题
难易度:较难
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
题号:3419576
题型:选择题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
题号:3419577
题型:选择题
难易度:较难
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】四棱锥
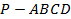
的底面
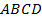
是边长为6的正方形,且
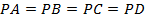
,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )
| A.6 | B.5 | C. | D. |
题号:3419578
题型:选择题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】已知函数
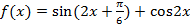
,则
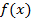
的一个单调递减区间是( )
题号:3419579
题型:选择题
难易度:一般
日期:2017-03-15
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】某几何体三视如下图,则该几何体体积是( )
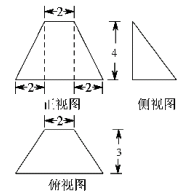
题号:3419580
题型:选择题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】李冶(1192-1279),真定栾城(今属河北石家庄市)人,金元时期的数学家、诗人、晚年在封龙山隐居
讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径,正方形的边长等,其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为

亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:
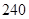
平方步为
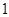
亩,圆周率按
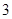
近似计算)
题号:3419581
题型:选择题
难易度:一般
日期:2017-03-15
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】执行下面的程序框图,则输出
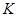
的值为 ( )
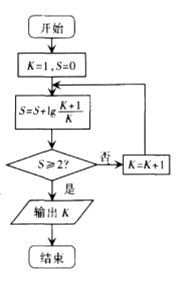
题号:3419582
题型:选择题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
题号:3419583
题型:选择题
难易度:较易
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】“
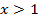
”是“

”的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
题号:3419584
题型:选择题
难易度:较易
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】在复平面中,复数
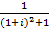
对应的点在( )
题号:3419585
题型:选择题
难易度:容易
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】设
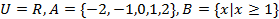
,则
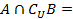
( )
题号:3419571
题型:填空题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】在

中,角

的对边分别为

,若

,

,

,

,则角

的大小为__________.
题号:3419572
题型:填空题
难易度:较易
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
题号:3419573
题型:填空题
难易度:容易
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】设样本数据
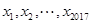
的方差是4,若
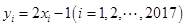
,则
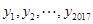
的方差为__________.
题号:3435009
题型:填空题
难易度:较难
日期:2017-03-20
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】非零向量
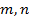
的夹角为

,且满足
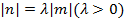
,向量组
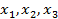
由一个
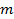
和两个
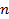
排列而成,向量组

由两个
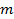
和一个
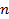
排列而成,若
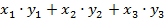
所有可能值中的最小值为
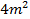
,则

__________.
题号:3419563
题型:解答题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】选修4-5:不等式选讲
设函数
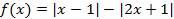
的最大值为
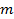
.
(1)作出函数
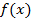
的图象;
(2)若
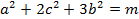
,求
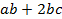
的最大值.
题号:3419564
题型:解答题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】选修4-4:坐标系与参数方程
在平面直角坐标系
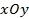
中,曲线
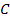
的参数方程为
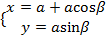
(
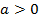
,
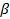
为参数),以坐标原点
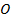
为极点,以
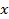
轴正半轴为极轴,建立极坐标系,直线
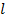
的极坐标方程
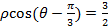
.
(1)若曲线
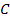
与
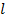
只有一个公共点,求
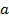
的值;
(2)
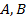
为曲线
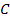
上的两点,且
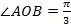
,求
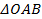
的面积最大值.
题号:3419565
题型:解答题
难易度:困难
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】已知函数
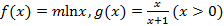
.
(1)当
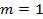
时,求曲线
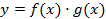
在
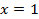
处的切线方程;
(2)讨论函数
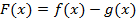
在
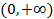
上的单调性.
题号:3419566
题型:解答题
难易度:较难
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】已知椭圆
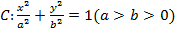
的左、右顶点分别为
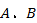
,且长轴长为8,
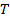
为椭圆上一点,直线
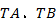
的斜率之积为
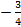
.
(1)求椭圆
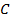
的方程;
(2)设
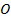
为原点,过点
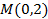
的动直线与椭圆
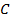
交于
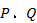
两点,求
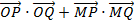
的取值范围.
题号:3419567
题型:解答题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为
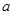
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表
|
| 浮动因素
| 浮动比率
|
| 上一个年度未发生有责任道路交通事故
| 下浮10%
|
| 上两个年度未发生有责任道路交通事故
| 下浮20%
|
| 上三个及以上年度未发生有责任道路交通事故
| 下浮30%
|
| 上一个年度发生一次有责任不涉及死亡的道路交通事故
| 0%
|
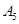
| 上一个年度发生两次及两次以上有责任道路交通事故
| 上浮10%
|

| 上一个年度发生有责任道路交通死亡事故
| 上浮30%
|
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,
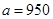
,记
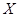
为某同学家的一辆该品牌车在第四年续保时的费用,求
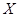
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
题号:3419568
题型:解答题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
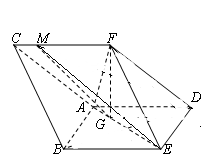
【题文】如图,三棱柱
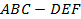
中,侧面
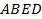
是边长为2的菱形,且
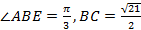
.点
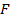
在平面
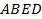
内的正投影为
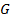
,且
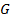
在
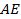
上,
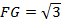
,点
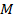
在线段
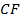
上,且
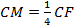
.
(1)证明:直线
平面
;
(2)求三棱锥
的体积.
题号:3419569
题型:解答题
难易度:一般
日期:2017-03-14
来源:【全国市级联考】2017届河北省石家庄市高三第二次质量检测数学(文)试卷(带解析)
【题文】已知等差数列
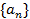
的前
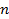
项和为
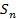
,若
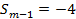
,
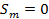
,
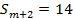
(
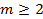
且
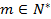
).
(1)求
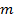
的值;
(2)若数列
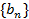
满足
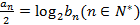
,求数列
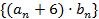
的前
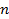
项和.
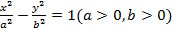 的左右焦点分别为
的左右焦点分别为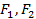 ,过点
,过点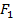 且垂直于
且垂直于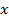 轴的直线与该双曲线的左支交于
轴的直线与该双曲线的左支交于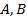 两点,
两点,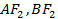 分别交
分别交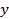 轴于
轴于 两点,若
两点,若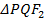 的周长为12,则
的周长为12,则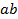 取得最大值时该双曲线的离心率为( )
取得最大值时该双曲线的离心率为( )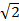
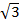
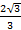
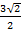
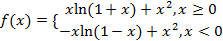 ,若
,若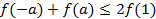 ,则实数
,则实数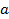 的取值范围是( )
的取值范围是( )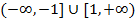
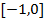
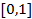
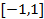
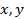 满足约束条件
满足约束条件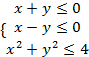 ,则
,则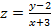 的最小值为 ( )
的最小值为 ( )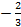
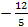
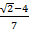
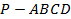 的底面
的底面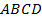 是边长为6的正方形,且
是边长为6的正方形,且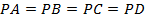 ,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )
,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )

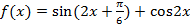 ,则
,则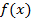 的一个单调递减区间是( )
的一个单调递减区间是( )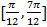
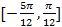
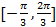
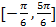

 亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:
亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注: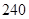 平方步为
平方步为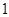 亩,圆周率按
亩,圆周率按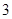 近似计算)
近似计算)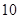 步、
步、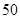 步
步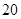 步、
步、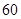 步
步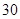 步、
步、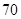 步
步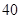 步、
步、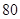 步
步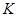 的值为 ( )
的值为 ( )
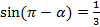 ,且
,且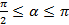 ,则
,则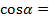 ( )
( )

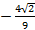

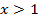 ”是“
”是“ ”的( )
”的( )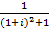 对应的点在( )
对应的点在( )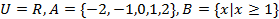 ,则
,则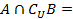 ( )
( )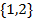
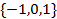
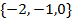
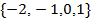
 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,
, ,则角
,则角 的大小为__________.
的大小为__________.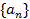 中,若
中,若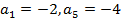 ,则
,则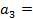 __________.
__________.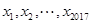 的方差是4,若
的方差是4,若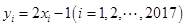 ,则
,则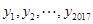 的方差为__________.
的方差为__________.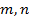 的夹角为
的夹角为 ,且满足
,且满足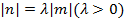 ,向量组
,向量组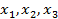 由一个
由一个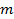 和两个
和两个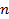 排列而成,向量组
排列而成,向量组 由两个
由两个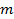 和一个
和一个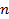 排列而成,若
排列而成,若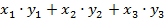 所有可能值中的最小值为
所有可能值中的最小值为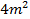 ,则
,则 __________.
__________.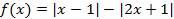 的最大值为
的最大值为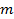 .
. 的图象;
的图象;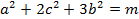 ,求
,求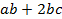 的最大值.
的最大值. 中,曲线
中,曲线 的参数方程为
的参数方程为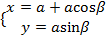 (
(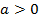 ,
,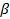 为参数),以坐标原点
为参数),以坐标原点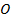 为极点,以
为极点,以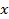 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线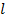 的极坐标方程
的极坐标方程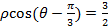 .
.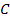 与
与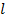 只有一个公共点,求
只有一个公共点,求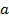 的值;
的值;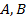 为曲线
为曲线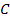 上的两点,且
上的两点,且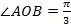 ,求
,求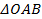 的面积最大值.
的面积最大值.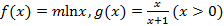 .
.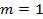 时,求曲线
时,求曲线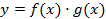 在
在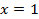 处的切线方程;
处的切线方程;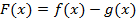 在
在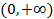 上的单调性.
上的单调性.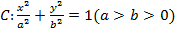 的左、右顶点分别为
的左、右顶点分别为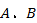 ,且长轴长为8,
,且长轴长为8,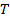 为椭圆上一点,直线
为椭圆上一点,直线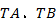 的斜率之积为
的斜率之积为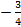 .
.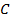 的方程;
的方程; 为原点,过点
为原点,过点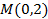 的动直线与椭圆
的动直线与椭圆 交于
交于 两点,求
两点,求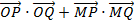 的取值范围.
的取值范围. 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
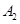
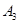
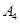
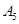

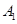
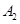
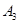
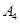
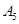

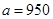 ,记
,记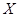 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求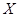 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)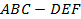 中,侧面
中,侧面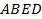 是边长为2的菱形,且
是边长为2的菱形,且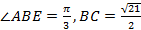 .点
.点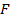 在平面
在平面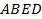 内的正投影为
内的正投影为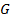 ,且
,且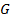 在
在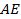 上,
上,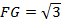 ,点
,点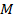 在线段
在线段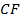 上,且
上,且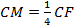 .
.
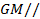 平面
平面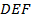 ;
;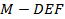 的体积.
的体积.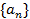 的前
的前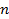 项和为
项和为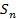 ,若
,若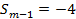 ,
,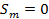 ,
,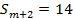 (
(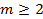 且
且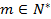 ).
).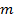 的值;
的值;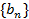 满足
满足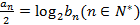 ,求数列
,求数列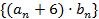 的前
的前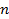 项和.
项和.