适用年级:{{getGradeNameByProperty('高三|高考模拟|重庆|2017年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|重庆|2017年')}} 使用省份:{{getAreaName('高三|高考模拟|重庆|2017年')}}
试卷年份:{{getYear('高三|高考模拟|重庆|2017年')}}上传日期:2017-06-05题数:23
提示:单击题文可显示答案与解析。
题号:3749423
题型:选择题
难易度:一般
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】设
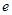
表示自然对数的底数,函数
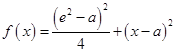
(
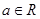
),若关于
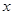
的不等式
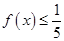
有解,则实数
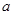
的值为( )
题号:3749424
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】设抛物线
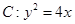
的焦点为
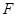
,过点
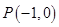
作斜率为
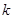
(
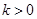
)的直线
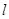
与抛物线
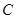
交于
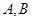
两点,若
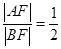
,则
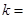
( )
A.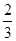 | B.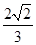 | C.1 | D.2 |
题号:3749425
题型:选择题
难易度:一般
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】已知三棱锥
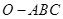
的顶点
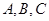
都在半径为3的球面上,
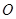
是球心,
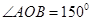
,当
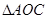
与
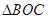
的面积之和最大时,三棱锥
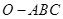
的体积为( )
题号:3749426
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
题号:3749427
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
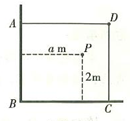
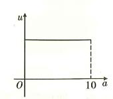
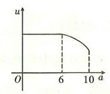
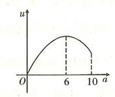
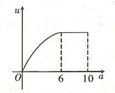
【题文】如图,一直角墙角的两边足够长,若
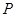
处有一棵树(不考虑树的粗细)与两墙的距离分别是
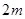
和
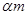
(
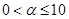
),现用
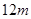
长的篱笆,借助墙角围成一个矩形花圃
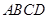
,设此矩形花圃的最大面积为
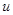
,若将这棵树围在矩形花圃内(包括边界),则函数
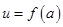
(单位:
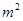
)的图象大致是( )
题号:3749428
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】我国魏晋时期的数学家刘徽在《九章算术注》中首创割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,即通过圆内接正多边形割圆,通过逐步增加正多边形的边数而使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率,如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中
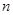
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(数据
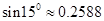
,
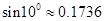
,
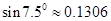
)
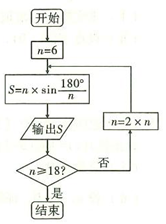
| A.3,3.1248,3.1320 | B.3,3.1056,3.1248 |
| C.3,3.1056,3.1320 | D.3,3.1,3.140 |
题号:3749463
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )
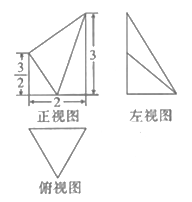
题号:3749464
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】函数
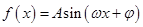
(
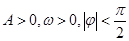
)的图象如图所示,将
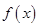
的图象向右平移
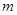
个单位得到
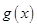
的图象关于
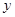
轴对称,则正数
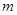
的最小值为( )
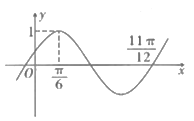
题号:3749468
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】若圆
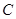
与
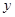
轴相切于点
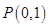
,与
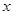
轴的正半轴交于
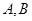
两点,且
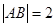
,则圆
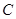
的标准方程是( )
题号:3749469
题型:选择题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】已知数列
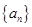
是递增的等比数列,
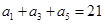
,
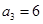
,则
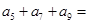
( )
A.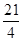 | B.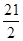 | C.42 | D.84 |
题号:3749470
题型:选择题
难易度:容易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
题号:3749472
题型:选择题
难易度:容易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
题号:3749419
题型:填空题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】已知正项数列
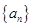
满足
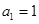
,
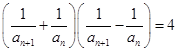
,数列
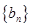
满足
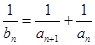
,记
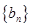
的前
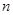
项和为
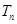
,则
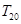
的值为__________.
题号:3749420
题型:填空题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】若星期一的所温为20℃,人星期二开始,每天的气温与前一天相比,仅等可能存在三种情形:“升
1℃”、“持平”、“降1℃”,则星期五时气温也为20℃的概率为__________.
题号:3749421
题型:填空题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】在
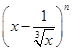
展开式中,只有第7项的二项式系数最大,则展开式中常数项是__________.
题号:3749422
题型:填空题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】已知
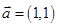
,
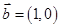
,则当
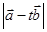
取最小值时,实数
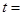
__________.
题号:3749415
题型:解答题
难易度:一般
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】已知
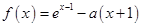
(
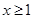
),
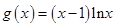
,其中
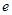
为自然对数的底数.
(1)若
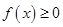
恒成立,求实数
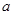
的取值范围;
(2)若在(1)的条件下,当
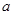
取最大值时,求证:
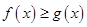
.
题号:3749416
题型:解答题
难易度:一般
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】已知椭圆
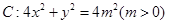
,过原点的直线与椭圆
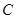
交于
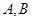
两点,点
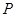
是椭圆上的任意一点且直线
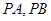
与坐标轴不平行.
(1)证明:直线
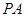
的斜率与直线
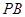
斜率之积为定值;
(2)若
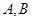
不是椭圆
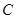
的顶点,且
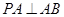
,直线
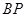
与
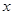
轴,
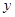
轴分别交于
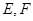
两点.
(i)证明:直线
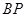
的斜率与直线
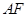
斜率之比为定值;
(ii)记
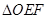
的面积为
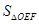
,求
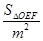
的最大值.
题号:3749417
题型:解答题
难易度:一般
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布
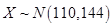
,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:

(注:表中试卷编号
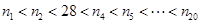
)
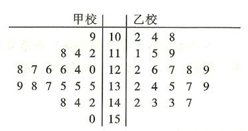
(1)列出表中试卷得分为126分的试卷编号(写出具体数据);
(2)该市又从乙校中也用系统抽样的方法抽取了20份试卷,将甲乙两校这40份试卷的得分制作了茎叶图(如图6),试通过茎叶图比较两校学生成绩的平均分及分散程度(均不要求计算出具体值,给出结论即可);
(3)在第(2)问的前提下,从甲乙两校这40名学生中,从成绩在140分以上(含140分)的学生中任意抽取3人,该3人在全市前15名的人数记为
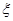
,求
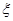
的分布列和期望.
(附:若随机变量
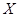
服从正态分布
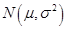
,则
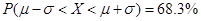
,
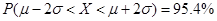
,
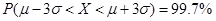
)
题号:3749418
题型:解答题
难易度:一般
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】如图所示,正三角形
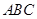
所在平面与梯形
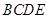
所在平面垂直,
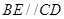
,
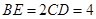
,
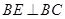
,
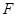
为棱
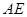
的中点.
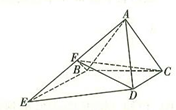
(1)求证:直线
平面
;
(2)若异面直线
与
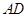
所成角为
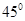
,求二面角

的余弦值.
题号:3749429
题型:解答题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】选修4-5:不等式选讲
设函数
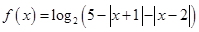
的定义域为
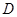
.
(1)求集合
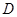
;
(2)设
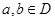
,证明:
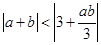
.
题号:3749434
题型:解答题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】已知锐角
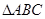
的三个内角
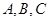
的对边分别为
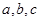
,且
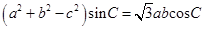
.
(1)求角
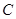
;
(2)若
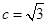
,求
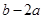
的取值范围.
题号:3749437
题型:解答题
难易度:较易
日期:2017-06-05
来源:【全国百强校】重庆市第八中学2017届高三高考适应性月考卷(八)理科数学试题
【题文】选修4-4:坐标系与参数方程
在平面直角系
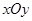
中,以原点为极点,
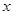
轴正半轴为极轴建立极坐标系,已知曲线
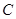
的极坐标为
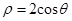
,且直线
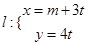
(
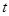
为参数)与曲线
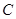
交于不同两点
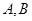
.
(1)求实数
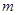
的取值范围;
(2)设点
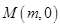
,若
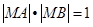
,求实数
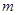
的值.
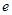 表示自然对数的底数,函数
表示自然对数的底数,函数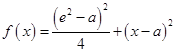 (
(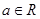 ),若关于
),若关于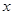 的不等式
的不等式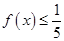 有解,则实数
有解,则实数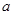 的值为( )
的值为( )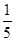
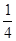
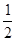
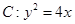 的焦点为
的焦点为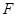 ,过点
,过点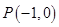 作斜率为
作斜率为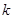 (
(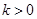 )的直线
)的直线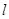 与抛物线
与抛物线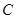 交于
交于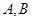 两点,若
两点,若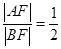 ,则
,则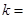 ( )
( )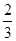
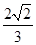
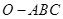 的顶点
的顶点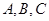 都在半径为3的球面上,
都在半径为3的球面上,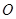 是球心,
是球心,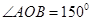 ,当
,当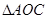 与
与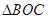 的面积之和最大时,三棱锥
的面积之和最大时,三棱锥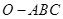 的体积为( )
的体积为( )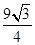
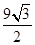
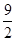
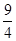
 满足
满足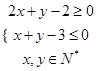 ,则
,则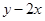 的最大值为( )
的最大值为( )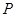 处有一棵树(不考虑树的粗细)与两墙的距离分别是
处有一棵树(不考虑树的粗细)与两墙的距离分别是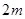 和
和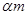 (
(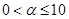 ),现用
),现用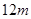 长的篱笆,借助墙角围成一个矩形花圃
长的篱笆,借助墙角围成一个矩形花圃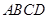 ,设此矩形花圃的最大面积为
,设此矩形花圃的最大面积为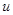 ,若将这棵树围在矩形花圃内(包括边界),则函数
,若将这棵树围在矩形花圃内(包括边界),则函数 (单位:
(单位: )的图象大致是( )
)的图象大致是( )
 表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(数据
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(数据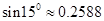 ,
,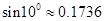 ,
,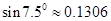 )
)

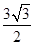
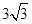
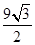
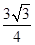
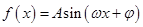 (
(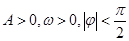 )的图象如图所示,将
)的图象如图所示,将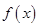 的图象向右平移
的图象向右平移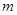 个单位得到
个单位得到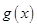 的图象关于
的图象关于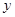 轴对称,则正数
轴对称,则正数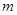 的最小值为( )
的最小值为( )
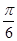
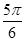
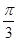
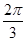
 与
与 轴相切于点
轴相切于点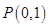 ,与
,与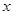 轴的正半轴交于
轴的正半轴交于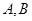 两点,且
两点,且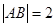 ,则圆
,则圆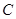 的标准方程是( )
的标准方程是( )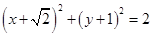
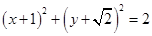
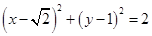
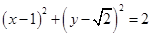
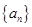 是递增的等比数列,
是递增的等比数列,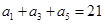 ,
,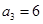 ,则
,则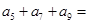 ( )
( )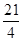
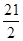
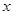 是实数,
是实数,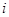 是虚数单位 ,且
是虚数单位 ,且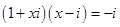 ,则
,则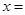 ( )
( )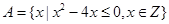 ,
,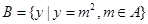 ,则
,则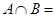 ( )
( )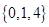
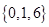
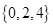
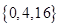
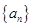 满足
满足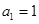 ,
,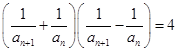 ,数列
,数列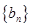 满足
满足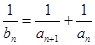 ,记
,记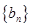 的前
的前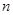 项和为
项和为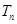 ,则
,则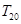 的值为__________.
的值为__________.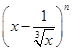 展开式中,只有第7项的二项式系数最大,则展开式中常数项是__________.
展开式中,只有第7项的二项式系数最大,则展开式中常数项是__________.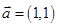 ,
,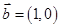 ,则当
,则当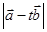 取最小值时,实数
取最小值时,实数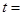 __________.
__________.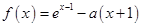 (
(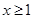 ),
),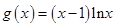 ,其中
,其中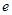 为自然对数的底数.
为自然对数的底数.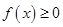 恒成立,求实数
恒成立,求实数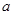 的取值范围;
的取值范围;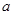 取最大值时,求证:
取最大值时,求证: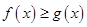 .
.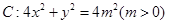 ,过原点的直线与椭圆
,过原点的直线与椭圆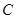 交于
交于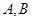 两点,点
两点,点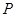 是椭圆上的任意一点且直线
是椭圆上的任意一点且直线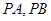 与坐标轴不平行.
与坐标轴不平行.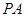 的斜率与直线
的斜率与直线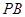 斜率之积为定值;
斜率之积为定值;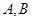 不是椭圆
不是椭圆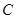 的顶点,且
的顶点,且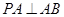 ,直线
,直线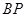 与
与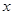 轴,
轴,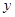 轴分别交于
轴分别交于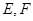 两点.
两点.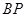 的斜率与直线
的斜率与直线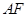 斜率之比为定值;
斜率之比为定值;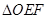 的面积为
的面积为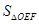 ,求
,求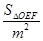 的最大值.
的最大值.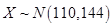 ,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
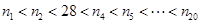 )
)
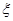 ,求
,求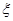 的分布列和期望.
的分布列和期望.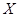 服从正态分布
服从正态分布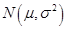 ,则
,则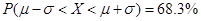 ,
,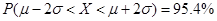 ,
,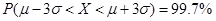 )
) 所在平面与梯形
所在平面与梯形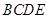 所在平面垂直,
所在平面垂直,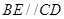 ,
,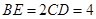 ,
,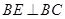 ,
,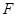 为棱
为棱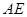 的中点.
的中点.
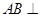 平面
平面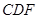 ;
;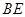 与
与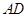 所成角为
所成角为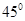 ,求二面角
,求二面角 的余弦值.
的余弦值.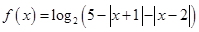 的定义域为
的定义域为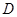 .
.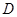 ;
;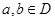 ,证明:
,证明: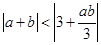 .
.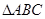 的三个内角
的三个内角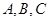 的对边分别为
的对边分别为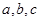 ,且
,且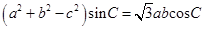 .
.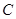 ;
;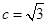 ,求
,求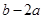 的取值范围.
的取值范围.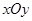 中,以原点为极点,
中,以原点为极点,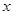 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线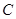 的极坐标为
的极坐标为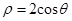 ,且直线
,且直线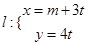 (
(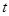 为参数)与曲线
为参数)与曲线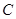 交于不同两点
交于不同两点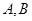 .
.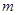 的取值范围;
的取值范围;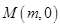 ,若
,若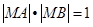 ,求实数
,求实数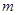 的值.
的值.