适用年级:{{getGradeNameByProperty('高三|高考模拟|江苏|2015年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|江苏|2015年')}} 使用省份:{{getAreaName('高三|高考模拟|江苏|2015年')}}
试卷年份:{{getYear('高三|高考模拟|江苏|2015年')}}上传日期:2015-04-22题数:26
提示:单击题文可显示答案与解析。
题号:842805
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】已知函数
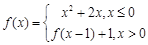
,当
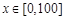
时,关于
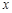
的方程
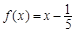
的所有解的和为
.
题号:842806
题型:填空题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
题号:842807
题型:填空题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】在平面直角坐标系
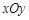
中,已知⊙C:
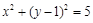
,A为⊙C与x轴负半轴的交点,过A作⊙C的弦AB,记线段AB的中点为M . 若OA = OM,则直线AB的斜率为
.
题号:842808
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
题号:842809
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】记等差数列
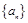
的前n项和为
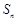
.已知
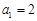
,且数列
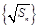
也为等差数列,则
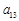
的值为
.
题号:842810
题型:填空题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】在平面直角坐标系xOy中,已知抛物线C:
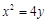
的焦点为F,定点
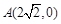
.若射线FA与抛物线C 相交于点M,与抛物线C的准线相交于点N,则FM:MN的值是
.
题号:842811
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
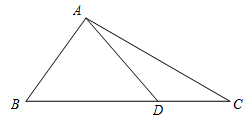
【题文】如图,在
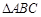
中,D是BC上的一点.已知
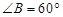
,
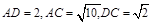
,则AB=
.
题号:842852
题型:填空题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】已知平面α,β,直线
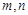
.给出下列命题:
① 若
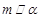
,
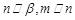
,则
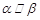
;
② 若
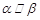
,
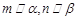
,则
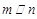
;
③ 若
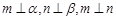
,则
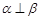
;
④ 若
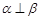
,
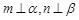
,则
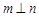
.
其中是真命题的是
.(填写所有真命题的序号).
题号:842853
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
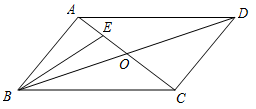
【题文】如图,在平面四边形ABCD中,AC,BD相交于点O,E为线段AO的中点.若
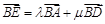
(
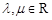
),则
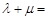
.
题号:842854
题型:填空题
难易度:容易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】袋中有大小、质地相同的红、黑球各一个,现有放回地随机摸取3次,每次摸取一个球,若摸出红球,得2分,摸出黑球,得1分,则3次摸球所得总分至少是4分的概率是 .
题号:842855
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
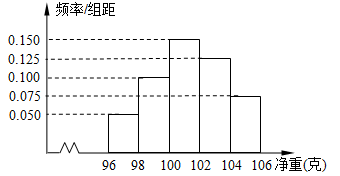
【题文】某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间
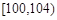
上的产品件数是
.
题号:842856
题型:填空题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
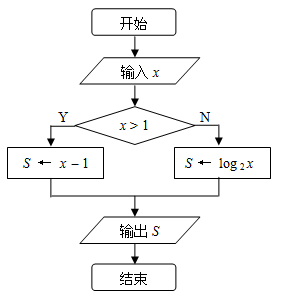
【题文】如图是一个算法流程图,如果输入
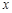
的值是
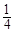
,则输出的
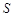
的值是
.
题号:842857
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】已知复数
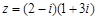
,其中
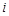
是虚数单位,则复数
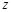
在复平面上对应的点位于第
象限.
题号:842858
题型:填空题
难易度:较易
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】函数
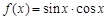
的最小正周期为
.
题号:842793
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】已知
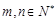
,定义
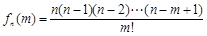
.
(1)记
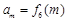
,求
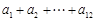
的值;
(2)记
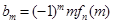
,求
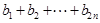
所有可能值的集合.
题号:842795
题型:解答题
难易度:较难
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】选修4-5:不等式选讲
已知x,y,z都是正数,且xyz = 1,求证:(1+x)(1+y)(1+z) ≥ 8.
题号:842796
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C:
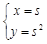
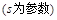
,直线l:
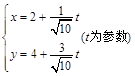
.设曲线C 与直线l交于A,B两点,求线段AB的长度.
题号:842797
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】选修4-2:矩阵与变换
已知矩阵
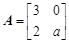
,A的逆矩阵
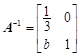
.
(1)求a,b的值;(2)求A的特征值.
题号:842798
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】选修4-1:几何证明选讲
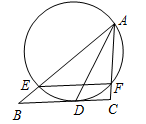
如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,
求证:EF∥BC.
题号:842799
题型:解答题
难易度:较难
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】给定一个数列
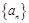
,在这个数列里,任取
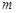
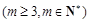
项,并且不改变它们在数列
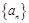
中的先后次序,得到的数列
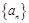
的一个
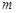
阶子数列.
已知数列
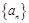
的通项公式为
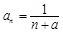
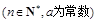
,等差数列
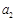
,
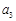
,
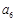
是数列
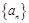
的一个3阶子数列.
(1)求
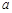
的值;
(2)等差数列
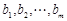
是
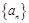
的一个
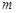
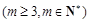
阶子数列,且
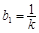
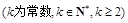
,求证:
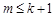
;
(3)等比数列
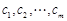
是
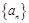
的一个
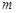
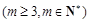
阶子数列,求证:
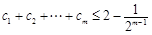
.
题号:842800
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】已知函数
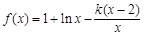
,其中
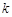
为常数.
(1)若
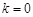
,求曲线
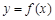
在点
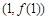
处的切线方程;
(2)若
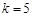
,求证:
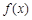
有且仅有两个零点;
(3)若
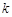
为整数,且当
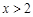
时,
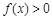
恒成立,求
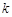
的最大值.
题号:842801
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】如图,在平面直角坐标系
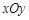
中,椭圆E:
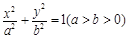
的离心率为
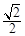
,直线l:
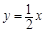
与椭圆E相交于A,B两点,
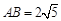
,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
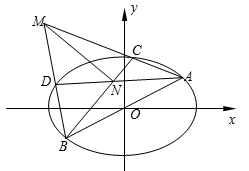
(1)求a,b的值;
(2)求证:直线MN的斜率为定值.
题号:842802
题型:解答题
难易度:较难
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
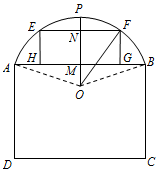
【题文】下图为某仓库一侧墙面的示意图,其下部是矩形ABCD,上部是圆弧AB,该圆弧所在的圆心为O,为了调节仓库内的湿度和温度,现要在墙面上开一个矩形的通风窗EFGH(其中E,F在圆弧AB上,G,H在弦AB上).过O作
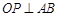
,交AB 于M,交EF于N,交圆弧AB于P,已知
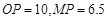
(单位:m),记通风窗EFGH的面积为S(单位:
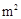
)
(1)按下列要求建立函数关系式:
(i)设
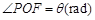
,将S表示成
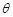
的函数;
(ii)设
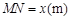
,将S表示成
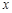
的函数;
(2)试问通风窗的高度MN为多少时,通风窗EFGH的面积S最大?
题号:842803
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】如图,在四棱锥P-ABCD中,
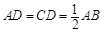
,
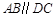
,
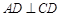
,
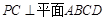
.
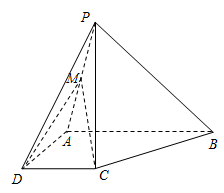
(1)求证:
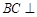
平面
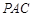
;
(2)若M为线段PA的中点,且过
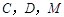
三点的平面与PB交于点N,求PN:PB的值.
题号:842804
题型:解答题
难易度:一般
日期:2015-04-22
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】在
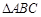
中,角A、B、C的对边分别为
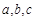
.已知
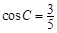
.
(1)若
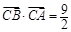
,求
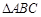
的面积;
(2)设向量
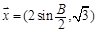
,
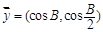
,且
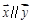
,求
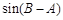
的值.
题号:4772297
题型:解答题
难易度:一般
日期:2017-07-28
来源:2015届江苏省南京市、盐城市高三第二次模拟考试数学试卷(带解析)
【题文】甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是
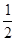
外,其余每局比赛甲队获胜的概率都是
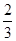
.假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
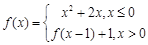 ,当
,当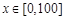 时,关于
时,关于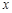 的方程
的方程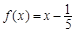 的所有解的和为 .
的所有解的和为 .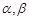 均为锐角,且
均为锐角,且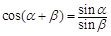 ,则
,则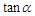 的最大值是 .
的最大值是 .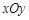 中,已知⊙C:
中,已知⊙C: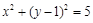 ,A为⊙C与x轴负半轴的交点,过A作⊙C的弦AB,记线段AB的中点为M . 若OA = OM,则直线AB的斜率为 .
,A为⊙C与x轴负半轴的交点,过A作⊙C的弦AB,记线段AB的中点为M . 若OA = OM,则直线AB的斜率为 .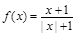 ,
,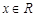 ,则不等式
,则不等式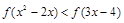 的解集是 .
的解集是 .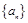 的前n项和为
的前n项和为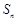 .已知
.已知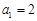 ,且数列
,且数列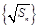 也为等差数列,则
也为等差数列,则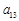 的值为 .
的值为 .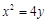 的焦点为F,定点
的焦点为F,定点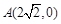 .若射线FA与抛物线C 相交于点M,与抛物线C的准线相交于点N,则FM:MN的值是 .
.若射线FA与抛物线C 相交于点M,与抛物线C的准线相交于点N,则FM:MN的值是 .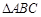 中,D是BC上的一点.已知
中,D是BC上的一点.已知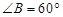 ,
,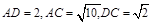 ,则AB= .
,则AB= .
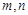 .给出下列命题:
.给出下列命题: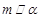 ,
,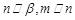 ,则
,则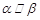 ;
; 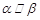 ,
,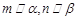 ,则
,则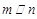 ;
;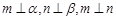 ,则
,则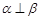 ;
; 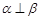 ,
,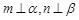 ,则
,则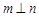 .
.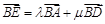 (
(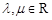 ),则
),则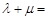 .
.
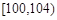 上的产品件数是 .
上的产品件数是 .
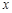 的值是
的值是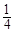 ,则输出的
,则输出的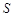 的值是 .
的值是 .
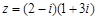 ,其中
,其中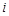 是虚数单位,则复数
是虚数单位,则复数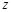 在复平面上对应的点位于第 象限.
在复平面上对应的点位于第 象限.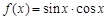 的最小正周期为 .
的最小正周期为 .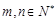 ,定义
,定义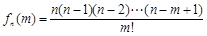 .
.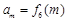 ,求
,求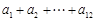 的值;
的值;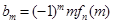 ,求
,求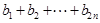 所有可能值的集合.
所有可能值的集合.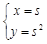
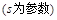 ,直线l:
,直线l: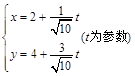 .设曲线C 与直线l交于A,B两点,求线段AB的长度.
.设曲线C 与直线l交于A,B两点,求线段AB的长度.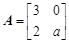 ,A的逆矩阵
,A的逆矩阵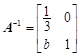 .
.
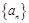 ,在这个数列里,任取
,在这个数列里,任取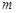
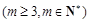 项,并且不改变它们在数列
项,并且不改变它们在数列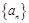 中的先后次序,得到的数列
中的先后次序,得到的数列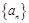 的一个
的一个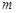 阶子数列.
阶子数列.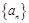 的通项公式为
的通项公式为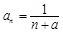
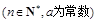 ,等差数列
,等差数列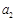 ,
,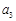 ,
,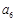 是数列
是数列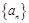 的一个3阶子数列.
的一个3阶子数列.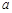 的值;
的值;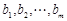 是
是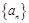 的一个
的一个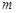
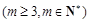 阶子数列,且
阶子数列,且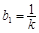
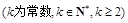 ,求证:
,求证: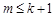 ;
;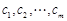 是
是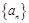 的一个
的一个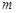
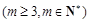 阶子数列,求证:
阶子数列,求证: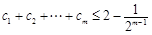 .
.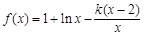 ,其中
,其中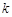 为常数.
为常数.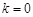 ,求曲线
,求曲线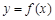 在点
在点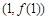 处的切线方程;
处的切线方程;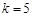 ,求证:
,求证: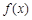 有且仅有两个零点;
有且仅有两个零点;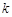 为整数,且当
为整数,且当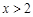 时,
时,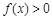 恒成立,求
恒成立,求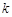 的最大值.
的最大值.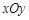 中,椭圆E:
中,椭圆E: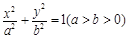 的离心率为
的离心率为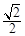 ,直线l:
,直线l: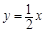 与椭圆E相交于A,B两点,
与椭圆E相交于A,B两点,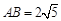 ,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
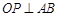 ,交AB 于M,交EF于N,交圆弧AB于P,已知
,交AB 于M,交EF于N,交圆弧AB于P,已知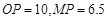 (单位:m),记通风窗EFGH的面积为S(单位:
(单位:m),记通风窗EFGH的面积为S(单位: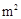 )
)
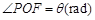 ,将S表示成
,将S表示成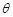 的函数;
的函数;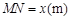 ,将S表示成
,将S表示成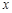 的函数;
的函数;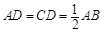 ,
,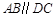 ,
,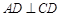 ,
,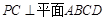 .
.
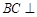 平面
平面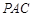 ;
;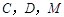 三点的平面与PB交于点N,求PN:PB的值.
三点的平面与PB交于点N,求PN:PB的值.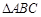 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为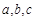 .已知
.已知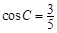 .
.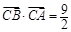 ,求
,求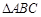 的面积;
的面积;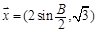 ,
,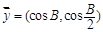 ,且
,且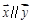 ,求
,求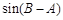 的值.
的值.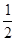 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是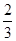 .假设各局比赛结果相互独立.
.假设各局比赛结果相互独立.