适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-05-29题数:16
提示:单击题文可显示答案与解析。
题号:916204
题型:选择题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】一个样本容量为10的样本数据,它们组成一个公差不为0的等差数列{a
n},若a
3=8且a
1,a
3,a
7成等比数列,则此样本的平均数和中位数分别是( )
| A.13,12 | B.13,13 | C.12,13 | D.13,14 |
题号:916205
题型:选择题
难易度:较易
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·厦门模拟)样本中共有五个个体,其值分别为a,0,1,2,3.若该样本的平均值为1,则样本方差为( )
题号:916206
题型:选择题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·黄石模拟)根据下面的列联表
| 嗜酒
| 不嗜酒
| 总计
|
患肝病
| 7 775
| 42
| 7 817
|
未患肝病
| 2 099
| 49
| 2 148
|
总计
| 9 874
| 91
| 9 965
|
得到如下几个判断:①在犯错误的概率不超过0.001的前提下认为患肝病与嗜酒有关;②在犯错误的概率不超过0.01的前提下认为患肝病与嗜酒有关;③认为患肝病与嗜酒有关的出错的可能小于1%;④认为患肝病与嗜酒有关的出错的可能为10%.其中正确命题的个数为( )
A.0 B.1 C.2 D.3
题号:916207
题型:选择题
难易度:较易
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·仙桃模拟)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )
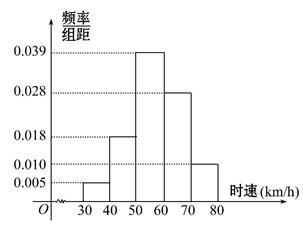
题号:916208
题型:选择题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】阅读程序框图,如果输出的函数值在区间
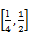
内,那么输入的实数x的取值范围是( )
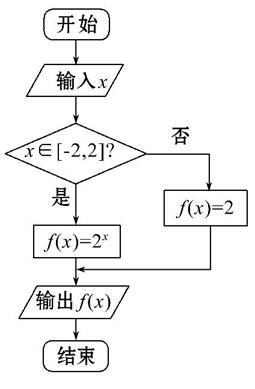
| A.(-∞,-2] | B.[-2,-1] | C.[-1,2] | D.[2,+∞) |
题号:916209
题型:选择题
难易度:较易
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·襄阳模拟)计算机执行如图的程序段后,输出的结果是( )
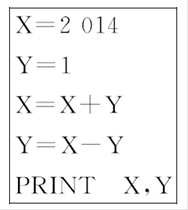
| A.2 015,2 013 | B.2 013,2 015 |
| C.2 015,2 015 | D.2 015,2 014 |
题号:3480258
题型:选择题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·宝鸡模拟)读程序回答问题
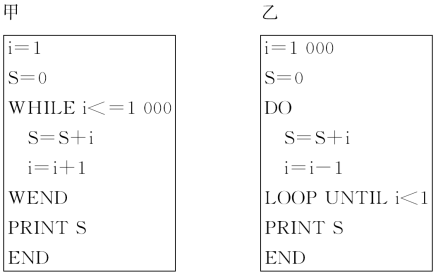
对甲、乙两程序和输出结果判断正确的是( )
| A.程序不同,结果不同 | B.程序不同,结果相同 |
| C.程序相同,结果不同 | D.程序相同,结果相同 |
题号:3480259
题型:选择题
难易度:较易
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】从某高中随机选取5名高三男生,其身高和体重的数据如表所示:
身高x(cm)
| 160
| 165
| 170
| 175
| 180
|
体重y(kg)
| 63
| 66
| 70
| 72
| 74
|
根据上表可得回归直线方程:
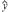
=0.56x+

,据此模型预报身高为172cm的高三男生的体重为( )
A.70.09kg B.70.12kg
C.70.55kg D.71.05kg
题号:916201
题型:填空题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】在2014年元旦期间,某市物价部门对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如表所示:
价格x
| 9
| 9.5
| 10
| 10.5
| 11
|
销售量y
| 11
| 10
| 8
| 6
| 5
|
通过分析,发现销售量y与商品的价格x具有线性相关关系,则销售量y关于商品的价格x的线性回归方程为__________.
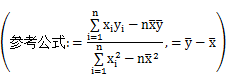
题号:916202
题型:填空题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
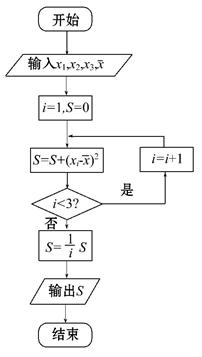
【题文】(2014·天门模拟)若执行如图所示的框图,输入x
1=1,x
2=2,x
3=3,

=2,则输出的数等于__________.
题号:916203
题型:填空题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·嘉兴模拟)在一次运动员的选拔中,测得7名选手身高(单位:cm)分布的茎叶图如图所示.已知记录的平均身高为164cm,但有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为__________.
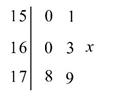
题号:3480260
题型:填空题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·沈阳模拟)甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了5次,成绩如下表(单位:环):
如果甲、乙两人中只有1人入选,那么入选的最佳人选应是__________.
题号:916198
题型:解答题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·郑州模拟)某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明:如图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.
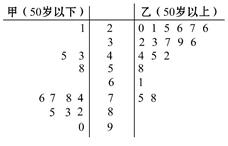
(1)根据茎叶图,帮助这位同学说明其亲属30人的饮食习惯.
(2)根据以上数据完成2×2列联表:
(3)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关,并写出简要分析.
题号:916199
题型:解答题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·黄冈模拟)某制造商3月生产了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如表:
分组
| 频数
| 频率
| 
|
[39.95,39.97)
| 10
|
|
|
[39.97,39.99)
| 20
|
|
|
[39.99,40.01)
| 50
|
|
|
[40.01,40.03]
| 20
|
|
|
合计
| 100
|
|
|
(1)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图.

(2)若以上述频率作为概率,已知标准乒乓球的直径为40.00mm,试求这批乒乓球的直径误差不超过0.03mm的概率.
(3)统计方法中,同一组数据常用该组区间的中点值(例如,区间[39.99,40.01)的中点值是40.00)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
题号:916200
题型:解答题
难易度:一般
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】(2014·长春模拟)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
甲
| 27
| 38
| 30
| 37
| 35
| 31
|
乙
| 33
| 29
| 38
| 34
| 28
| 36
|
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
题号:3480261
题型:解答题
难易度:较难
日期:2014-05-29
来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(带解析)
【题文】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期
| 1月
10日
| 2月
10日
| 3月
10日
| 4月
10日
| 5月
10日
| 6月
10日
|
昼夜温差
x(℃)
| 10
| 11
| 13
| 12
| 8
| 6
|
就诊人数
y(个)
| 22
| 25
| 29
| 26
| 16
| 12
|
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的概率.
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程
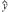
=

x+

.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式:

=
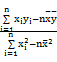
=
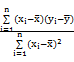
,

=

-


).
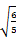

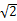

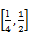 内,那么输入的实数x的取值范围是( )
内,那么输入的实数x的取值范围是( )
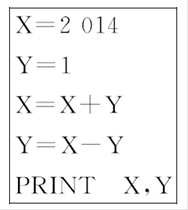

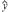 =0.56x+
=0.56x+ ,据此模型预报身高为172cm的高三男生的体重为( )
,据此模型预报身高为172cm的高三男生的体重为( )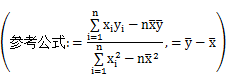
 =2,则输出的数等于__________.
=2,则输出的数等于__________.
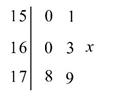



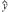 =
= x+
x+ .
. =
=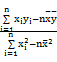 =
=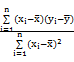 ,
, =
= -
-
 ).
).