适用年级:{{getGradeNameByProperty('高三|高考模拟|北京|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|北京|2014年')}} 使用省份:{{getAreaName('高三|高考模拟|北京|2014年')}}
试卷年份:{{getYear('高三|高考模拟|北京|2014年')}}上传日期:2014-05-14题数:20
提示:单击题文可显示答案与解析。
题号:922067
题型:选择题
难易度:较难
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】若双曲线
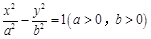
的渐近线与圆
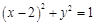
相切,则双曲线的离心率为( ).
题号:922068
题型:选择题
难易度:一般
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
题号:922069
题型:选择题
难易度:一般
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】在极坐标系中,点
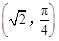
到直线
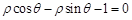
的距离等于( ).
题号:922070
题型:选择题
难易度:一般
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
题号:922071
题型:选择题
难易度:较易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
题号:922092
题型:选择题
难易度:容易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】复数
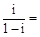
( ).
题号:922093
题型:选择题
难易度:较易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】已知集合
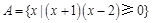
,则
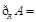
( ).
题号:3496390
题型:选择题
难易度:较难
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】已知符号函数
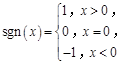
则函数
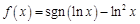
的零点个数为( ).
题号:922061
题型:填空题
难易度:一般
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
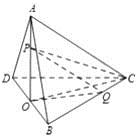
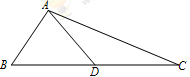
【题文】如图,在三棱锥
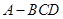
中,
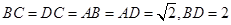
,平面
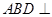
平面
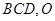
为
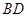
中点,
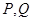
分别为线段
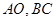
上的动点(不含端点),且
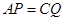
,则三棱锥
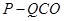
体积的最大值为_________.
题号:922062
题型:填空题
难易度:较易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】某写字楼将排成一排的6个车位出租给4个公司,其中有两个公司各有两辆汽车,如果这两个公司要求本公司的两个车位相邻,那么不同的分配方法共有________种.(用数字作答)
题号:922063
题型:填空题
难易度:较易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】已知函数
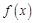
是定义在
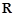
上的奇函数,当
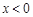
时,
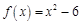
,则
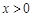
时,
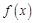
的解析式为______,不等式
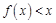
的解集为________.
题号:922064
题型:填空题
难易度:容易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】设不等式组
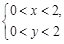
表示的平面区域为
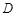
,在区域
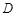
内随机取一个点
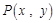
,则
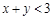
的概率为________.
题号:922065
题型:填空题
难易度:较易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
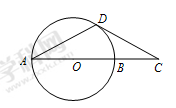
【题文】如图,
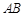
是圆
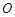
的直径,延长
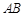
至
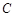
,使
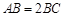
,且
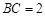
,
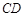
是圆
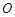
的切线,切点为
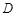
,连接
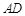
,则
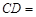
________,
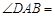
________.
题号:922066
题型:填空题
难易度:较易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】
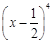
的二项展开式中常数项为________.(用数字作答)
题号:922055
题型:解答题
难易度:困难
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】已知集合
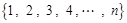
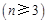
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
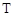
子集,记
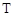
子集的个数为
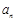
.
(1)当
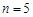
时,写出所有
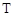
子集;
(2)求
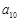
;
(3)记
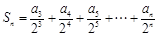
,求证:
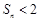
题号:922056
题型:解答题
难易度:较难
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】已知椭圆
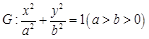
过点
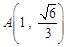
和点
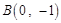
.
(1)求椭圆
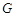
的方程;
(2)设过点
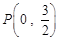
的直线
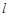
与椭圆
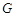
交于
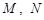
两点,且
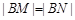
,求直线
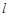
的方程.
题号:922057
题型:解答题
难易度:一般
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】已知函数
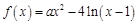
,
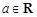
.
(1)当
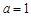
时,求
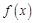
的单调区间;
(2)已知点
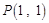
和函数
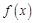
图象上动点
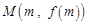
,对任意
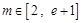
,直线
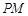
倾斜角都是钝角,求
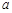
的取值范围.
题号:922058
题型:解答题
难易度:一般
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
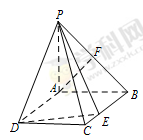
【题文】如图,在四棱锥
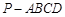
中,底面

为矩形,
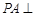
平面

,
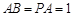
,
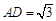
,
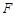
是
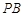
中点,
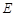
为
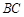
上一点.
(1)求证:
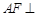
平面

;
(2)当
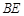
为何值时,二面角
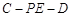
为
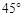
.
题号:922059
题型:解答题
难易度:一般
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间
的有8人.
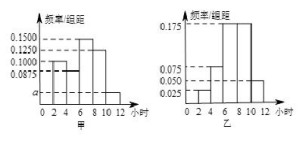
(1)求直方图中
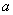
的值及甲班学生每天平均学习时间在区间
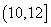
的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为
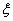
,求
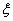
的分布列和数学期望.
题号:922060
题型:解答题
难易度:较易
日期:2014-05-14
来源:2014届北京市东城区高三下学期综合练习(一)理科数学试卷(带解析)
【题文】在
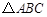
中,
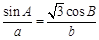
.
(1)求角
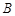
的值;
(2)如果
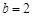
,求
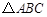
面积的最大值.
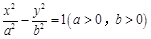 的渐近线与圆
的渐近线与圆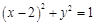 相切,则双曲线的离心率为( ).
相切,则双曲线的离心率为( ).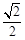
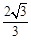
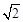
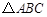 中,
中,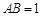 ,
,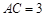 ,
,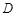 是
是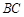 的中点,则
的中点,则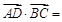 ( ).
( ).
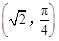 到直线
到直线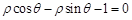 的距离等于( ).
的距离等于( ).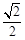
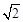
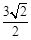
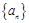 的前
的前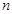 项和为
项和为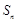 ,若
,若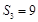 ,
,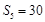 ,则
,则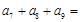 ( ).
( ).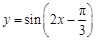 的图象,只需把函数
的图象,只需把函数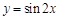 的图象( ).
的图象( ).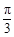 个单位长度
个单位长度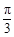 个单位长度
个单位长度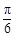 个单位长度
个单位长度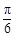 个单位长度
个单位长度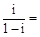 ( ).
( ).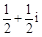
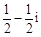
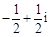
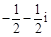
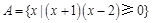 ,则
,则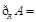 ( ).
( ).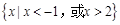
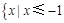 或
或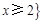
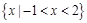
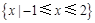
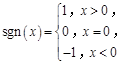 则函数
则函数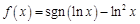 的零点个数为( ).
的零点个数为( ).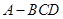 中,
中,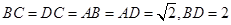 ,平面
,平面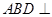 平面
平面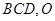 为
为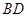 中点,
中点,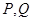 分别为线段
分别为线段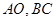 上的动点(不含端点),且
上的动点(不含端点),且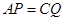 ,则三棱锥
,则三棱锥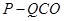 体积的最大值为_________.
体积的最大值为_________.
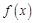 是定义在
是定义在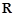 上的奇函数,当
上的奇函数,当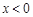 时,
时,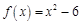 ,则
,则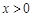 时,
时,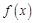 的解析式为______,不等式
的解析式为______,不等式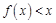 的解集为________.
的解集为________.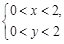 表示的平面区域为
表示的平面区域为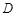 ,在区域
,在区域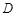 内随机取一个点
内随机取一个点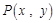 ,则
,则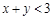 的概率为________.
的概率为________.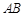 是圆
是圆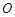 的直径,延长
的直径,延长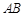 至
至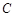 ,使
,使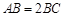 ,且
,且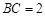 ,
,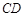 是圆
是圆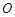 的切线,切点为
的切线,切点为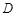 ,连接
,连接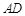 ,则
,则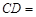 ________,
________,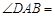 ________.
________.
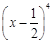 的二项展开式中常数项为________.(用数字作答)
的二项展开式中常数项为________.(用数字作答)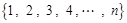
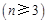 ,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为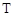 子集,记
子集,记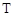 子集的个数为
子集的个数为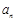 .
.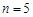 时,写出所有
时,写出所有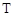 子集;
子集;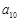 ;
;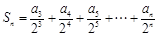 ,求证:
,求证: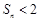
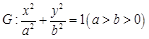 过点
过点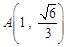 和点
和点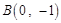 .
.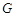 的方程;
的方程;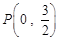 的直线
的直线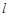 与椭圆
与椭圆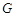 交于
交于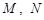 两点,且
两点,且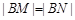 ,求直线
,求直线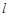 的方程.
的方程.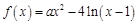 ,
,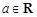 .
.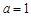 时,求
时,求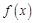 的单调区间;
的单调区间;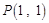 和函数
和函数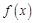 图象上动点
图象上动点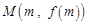 ,对任意
,对任意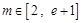 ,直线
,直线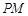 倾斜角都是钝角,求
倾斜角都是钝角,求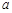 的取值范围.
的取值范围.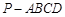 中,底面
中,底面 为矩形,
为矩形,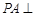 平面
平面 ,
,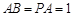 ,
,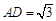 ,
,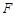 是
是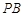 中点,
中点,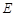 为
为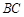 上一点.
上一点.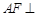 平面
平面 ;
;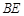 为何值时,二面角
为何值时,二面角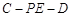 为
为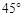 .
.
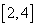 的有8人.
的有8人.
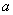 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间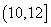 的人数;
的人数;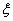 ,求
,求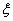 的分布列和数学期望.
的分布列和数学期望.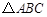 中,
中,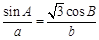 .
.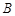 的值;
的值;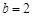 ,求
,求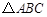 面积的最大值.
面积的最大值.