适用年级:{{getGradeNameByProperty('高三|专题试卷|安徽|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|安徽|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|安徽|2014年')}}
试卷年份:{{getYear('高三|专题试卷|安徽|2014年')}}上传日期:2014-03-31题数:21
提示:单击题文可显示答案与解析。
题号:942824
题型:选择题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知函数
y=
f(
x)的图象关于
y轴对称,且当
x∈(-∞,0)时,
f(
x)+
xf′(
x)<0成立,
a=(2
0.2)·
f(2
0.2),
b=(log
π3)·
f(log
π3),
c=(log
39)·
f(log
39),则
a,
b,
c的大小关系是( )
| A.b>a>c | B.c>a>b |
| C.c>b>a | D.a>c>b |
题号:942825
题型:选择题
难易度:较难
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知函数
f(
x)是定义在R上的奇函数,当
x<0时,
f(
x)=e
x(
x+1),给出下列命题:
①当
x>0时,
f(
x)=e
x(1-
x);②函数
f(
x)有两个零点;③
f(
x)>0的解集为(-1,0)∪(1,+∞);④∀
x1,
x2∈R,都有|
f(
x1)-
f(
x2)|<2.
其中正确命题的个数是( )
题号:942826
题型:选择题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】函数
y=
f(
x),
x∈
D,若存在常数
C,对任意的
x1∈
D,存在唯一的
x2∈
D使得
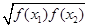
=
C,则称函数
f(
x)在
D上的几何平均数为
C.已知
f(
x)=
x3,
x∈[1,2],则函数
f(
x)=
x3在[1,2]上的几何平均数为( )
A.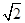 | B.2 |
| C.4 | D.2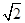 |
题号:942827
题型:选择题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知
f(
x)=3
2x-(
k+1)3
x+2,当
x∈R时,
f(
x)恒为正值,则
k的取值范围是( )
| A.(-∞,-1) | B.(-∞,2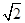 -1) -1) |
C.(-1,2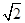 -1) -1) | D.(-2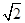 -1,2 -1,2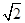 -1) -1) |
题号:942828
题型:选择题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】关于
x的不等式
x2-2
ax-8
a2<0(
a>0)的解集为(
x1,
x2),且
x2-
x1=15,则
a=( )
题号:942829
题型:选择题
难易度:较易
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】若
a,
b∈R,且
ab>0,则下列不等式中,恒成立的是( )
A.a+b≥2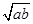 | B.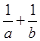 > >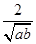 |
C.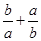 ≥2 ≥2 | D.a2+b2>2ab |
题号:942830
题型:选择题
难易度:较易
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】命题“若
a2+
b2=0,则
a=0且
b=0”的逆否命题是( )
| A.若a2+b2≠0,则a≠0且b≠0 | B.若a2+b2≠0,则a≠0或b≠0 |
| C.若a=0且b=0,则a2+b2≠0 | D.若a≠0或b≠0,则a2+b2≠0 |
题号:4187248
题型:选择题
难易度:一般
日期:2014-04-01
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】下列函数中,与函数
y=-3
|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是( )
A.y=-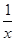 | B.y=log2|x| |
| C.y=1-x2 | D.y=x3-1 |
题号:4187249
题型:选择题
难易度:较易
日期:2014-04-01
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知
e1,
e2是两个单位向量,其夹角为
θ,若向量
m=2
e1+3
e2,则|
m|=1的充要条件是( )
题号:4187250
题型:选择题
难易度:较易
日期:2014-04-01
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】设
z=
x+
y,其中实数
x,
y满足
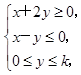
若
z的最大值为6,则
z的最小值为( )
题号:942819
题型:填空题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】设函数
f(
x)的定义域为
D,若存在非零实数
l使得对于任意
x∈
M(
M⊆
D),有
x+
l∈
D,且
f(
x+
l)≥
f(
x),则称函数
f(
x)为
M上的
l高调函数.现给出下列命题:
①函数
f(
x)=
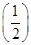 x
x是R上的1高调函数;
②函数
f(
x)=sin 2
x为R上的π高调函数;
③如果定义域为[-1,+∞)的函数
f(
x)=
x2为[-1,+∞)上的
m高调函数,那么实数
m的取值范围是[2,+∞).
其中正确的命题是________.(写出所有正确命题的序号)
题号:942820
题型:填空题
难易度:较易
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知集合
A、
B,定义集合
A与
B的一种运算
A⊕
B,其结果如下表所示:
A
| {1,2,3,4}
| {-1,1}
| {-4,8}
| {-1,0,1}
|
B
| {2,3,6}
| {-1,1}
| {-4,-2,0,2}
| {-2,-1,0,1}
|
A⊕B
| {1,4,6}
| ∅
| {-2,0,2,8}
| {-2}
|
按照上述定义,若
M={-2 011,0,2 012},
N={-2 012,0,2 013},则
M⊕
N=________.
题号:942821
题型:填空题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】设函数f(x)=ax+b(0≤x≤1),则a+2b>0是f(x)>0在[0,1]上恒成立的________条件.(填充分但不必要,必要但不充分,充要,既不充分也不必要)
题号:942822
题型:填空题
难易度:容易
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知集合A={x|x2-x≤0},函数f(x)=2-x(x∈A)的值域为B,则(∁RA)∩B=________.
题号:942823
题型:填空题
难易度:较易
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】函数g(x)=x2-2 013x,若g(a)=g(b),a≠b,则g(a+b)=________.
题号:942813
题型:解答题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知函数f(x)=ax2-ln x,x∈(0,e],其中e是自然对数的底数,a∈R.
(1)当a=1时,求函数f(x)的单调区间与极值;
(2)是否存在实数a,使f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由.
题号:942814
题型:解答题
难易度:较难
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】设函数
f(
x)=
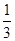 x3
x3-
ax2-
ax,
g(
x)=2
x2+4
x+
c.
(1)试问函数
f(
x)能否在
x=-1时取得极值?说明理由;
(2)若
a=-1,当
x∈[-3,4]时,函数
f(
x)与
g(
x)的图象有两个公共点,求
c的取值范围.
题号:942815
题型:解答题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】设函数
f(
x)=
ax2+
bx+
c,且
f(1)=-
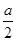
,3
a>2
c>2
b,求证:
(1)
a>0,且-3<
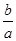
<-
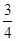
;
(2)函数
f(
x)在区间(0,2)内至少有一个零点;
(3)设
x1,
x2是函数
f(
x)的两个零点,则
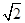
≤|
x1-
x2|<
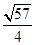
.
题号:942816
题型:解答题
难易度:较难
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知函数
f(
x)=ln
x+
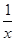
-1.
(1)求函数
f(
x)的单调区间;
(2)设
m∈R,对任意的
a∈(-1,1),总存在
x0∈[1,e],使得不等式
ma-
f(
x0)<0成立,求实数
m的取值范围.
题号:942817
题型:解答题
难易度:较难
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】已知函数
f(
x)=
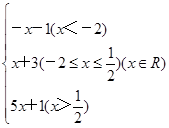
.
(1)求函数
f(
x)的最小值;
(2)已知
m∈R,命题
p:关于
x的不等式
f(
x)≥
m2+2
m-2对任意
m∈R恒成立;
q:函数
y=(
m2-1)
x是增函数.若“
p或
q”为真,“
p且
q”为假,求实数
m的取值范围.
题号:942818
题型:解答题
难易度:一般
日期:2014-03-31
来源:2014届(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(带解析)
【题文】设定义在(0,+∞)上的函数
f(
x)=
ax+
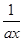
+
b(
a>0).
(1)求
f(
x)的最小值;
(2)若曲线
y=
f(
x)在点(1,
f(1))处的切线方程为
y=
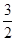 x
x,求
a,
b的值.
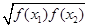 =C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
=C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )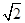
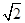
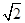 -1)
-1) 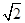 -1)
-1) 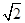 -1,2
-1,2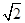 -1)
-1)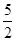
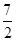
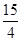
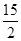
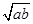
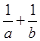 >
>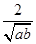
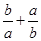 ≥2
≥2 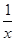
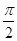
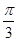
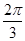
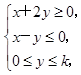 若z的最大值为6,则z的最小值为( )
若z的最大值为6,则z的最小值为( ) 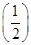 x是R上的1高调函数;
x是R上的1高调函数;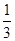 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.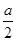 ,3a>2c>2b,求证:
,3a>2c>2b,求证: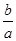 <-
<-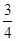 ;
;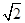 ≤|x1-x2|<
≤|x1-x2|<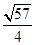 .
.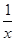 -1.
-1.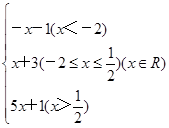 .
.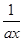 +b(a>0).
+b(a>0).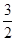 x,求a,b的值.
x,求a,b的值.