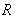 上的奇函数
上的奇函数 ,当
,当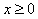 时,
时,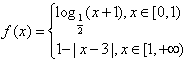 ,则关于
,则关于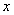 的函数
的函数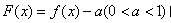 的所有零点之和为( )
的所有零点之和为( )A.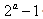 | B. | C.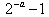 | D.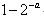 |
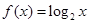 与函数
与函数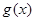 的图像关于
的图像关于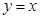 对称且有
对称且有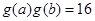 ,若
,若 ,则
,则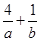 的最小值为( )
的最小值为( )| A.9 | B.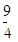 | C.4 | D.5 |
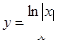 的图象大致是( )
的图象大致是( )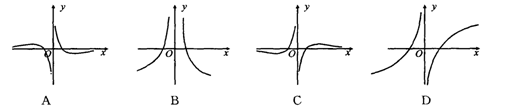
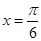 是函数
是函数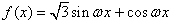 图象的一条对称轴,当
图象的一条对称轴,当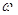 取最小正数时( )
取最小正数时( )A.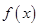 在 在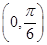 单调递增 单调递增 | B.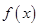 在 在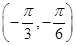 单调递减 单调递减 |
C.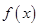 在 在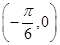 单调递减 单调递减 | D.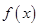 在 在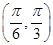 单调递增 单调递增 |
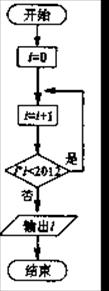
| A.43 | B.44 |
| C.45 | D.46 |
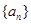 ,若点
,若点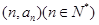 在经过点(5,3)的定直线
在经过点(5,3)的定直线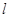 上,则数列
上,则数列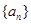 的前9项和
的前9项和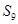 =( )
=( )| A.9 | B.10 | C.18 | D.27 |
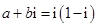 (其中
(其中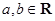 ,
,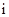 是虚数单位),则
是虚数单位),则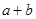 的值为( )
的值为( )A.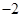 | B.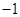 | C.0 | D.2 |
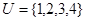 ,
,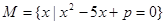 ,若
,若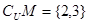 ,则实数
,则实数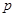 的值为( )
的值为( )A.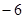 | B. | C.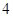 | D.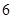 |
| | 相关人员数 | 抽取人数 |
| 公务员 | 35 | b |
| 教师 | a | 3 |
| 自由职业者 | 28 | 4 |
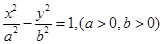 右支上一点,
右支上一点,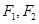 分别是双曲线的左、右焦点,I为
分别是双曲线的左、右焦点,I为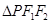 的内心,若
的内心,若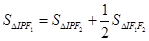 成立,则双曲线的离心率为( )
成立,则双曲线的离心率为( )| A.4 | B.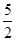 | C.2 | D.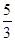 |
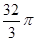 ,那么该三棱柱的体积是( )
,那么该三棱柱的体积是( )A.96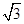 | B.16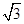 | C.24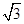 | D.48 |
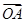 和
和 ,它们的夹角为
,它们的夹角为 ,点C在以O为圆心的圆弧AB上,且
,点C在以O为圆心的圆弧AB上,且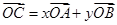 (其中
(其中 ),则满足
),则满足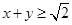 的概率为( )
的概率为( )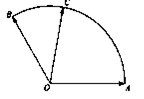
A.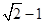 | B.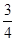 | C.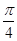 | D.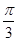 |
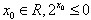 ”的否定是:“不存在
”的否定是:“不存在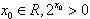 ”;
”;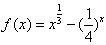 的零点在区间
的零点在区间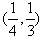 内;
内; 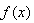 满足
满足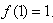 且
且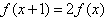 ,则
,则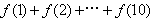 =1023;
=1023;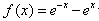 切线斜率的最大值是2.
切线斜率的最大值是2. (
(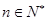 )定义其“调和均数倒数”
)定义其“调和均数倒数”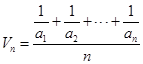 (
(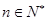 ),那么当
),那么当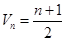 时,
时,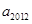 =_______________.
=_______________.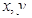 满足约束条件
满足约束条件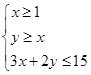
 ,则
,则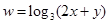 的最大值是________
的最大值是________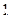 的圆,且这个几何体是球体的一部分,则这个几何体的表面积为 .
的圆,且这个几何体是球体的一部分,则这个几何体的表面积为 .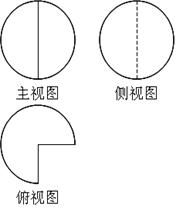
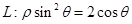 ,过点A(5,α)(α为锐角且
,过点A(5,α)(α为锐角且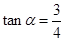 )作平行于
)作平行于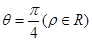 的直线
的直线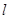 ,且
,且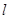 与曲线L分别交于B,C两点.
与曲线L分别交于B,C两点.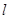 的普通方程;
的普通方程;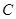 :
: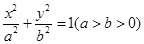 的离心率为
的离心率为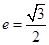 ,且过点
,且过点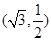 .
.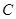 的标准方程;
的标准方程; 与椭圆
与椭圆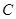 相交于
相交于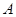 、
、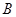 两点,若以
两点,若以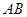 为直径的圆
为直径的圆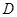 经过坐标原点.证明:圆
经过坐标原点.证明:圆 的半径为定值.
的半径为定值.
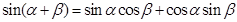 ------①
------①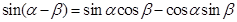 ------②
------②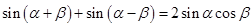 ------③
------③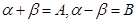 有
有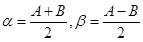
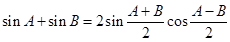 .
.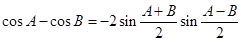 ;
;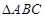 的三个内角
的三个内角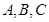 满足
满足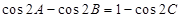 ,试判断
,试判断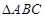 的形状.
的形状. =
=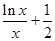 是否有实数解.
是否有实数解.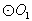 与
与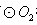 相交于A、B两点,AB是
相交于A、B两点,AB是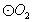 的直径,过A点作
的直径,过A点作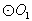 的切线交
的切线交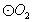 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与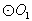 、
、 交于C,D两点.
交于C,D两点.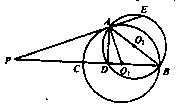
 (其中
(其中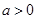 ).
).