适用年级:{{getGradeNameByProperty('高三|高考模拟|海南|2010年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|海南|2010年')}} 使用省份:{{getAreaName('高三|高考模拟|海南|2010年')}}
试卷年份:{{getYear('高三|高考模拟|海南|2010年')}}上传日期:2010-05-19题数:24
提示:单击题文可显示答案与解析。
题号:1279914
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】一个几何体的三视图如图所示,则该几何体的体积(单位:
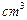
)为
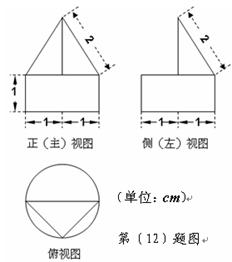
题号:1279915
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】已知函数
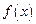
在
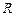
上满足
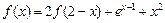
,则曲线
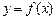
在点
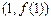
处的切线方程是
题号:1279916
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】如右图是高尔顿板的改造装置,当小球从
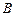
自由下落时,进入槽口
处的概率为

题号:1279917
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
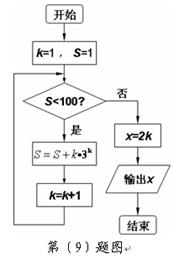
【题文】某程序框图如图所示,该程序运行后输出的
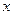
值是
题号:1279918
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
题号:1279919
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
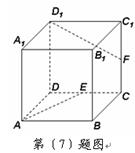
【题文】在正方体
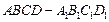
中,
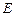
,
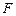
分别为
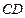
和
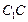
的中点,则直线
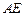
与
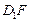
所成角的余弦值为
题号:1279920
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】设变量
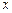
,
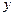
满足约束条件
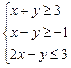
,则目标函数
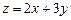
的最大值为
题号:1279921
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】12名同学进行队列训练,站成前排4人后排8人,现教官要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是
题号:1279922
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】已知
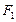
,
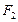
分别是双曲线
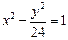
的左、右焦点,
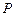
是双曲线上的一点,若
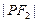
,
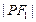
,
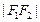
构成公差为正数的等差数列,则
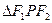
的面积为
题号:1279923
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】在△
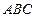
中,
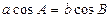
,则△
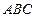
是
| A.等边三角形 | B.等腰直角三角形 |
| C.等腰三角形或直角三角形 | D.两直角边互不相等的直角三角形 |
题号:1279924
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】
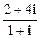
(
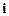
是虚数单位)的值是
题号:1279925
题型:选择题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
题号:1279910
题型:填空题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】用
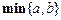
表示
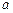
,
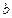
两个数中的最小值,设
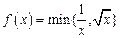
(
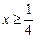
),则由函数
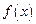
的图象,
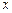
轴与直线
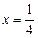
和直线
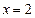
所围成的封闭图形的面积为_____
题号:1279911
题型:填空题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】若圆
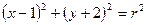
上有且只有两个点到直线
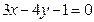
的距离等于1,则
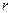
的取值范围是
题号:1279912
题型:填空题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】关于平面向量
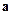
,
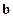
,
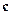
,有下列四个命题:
①若
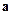
∥
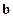
,
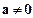
,
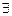
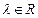
,使得
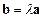
;
②若
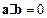
,则
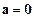
或
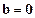
;
③存在不全为零的实数
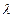
,
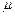
使得
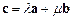
;
④若
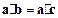
,则
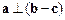
.
其中正确的命题序号是_________.
题号:1279913
题型:填空题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
题号:1279703
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—5:不等式选讲
设函数
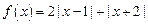
.
(Ⅰ)求不等式
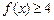
的解集;
(Ⅱ)若不等式
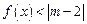
的解集是非空的集合,求实数
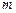
的取值范围.
题号:1279704
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的
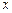
轴的正半轴重合.直线
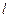
的参数方程是
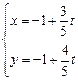
(
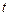
为参数),曲线
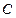
的极坐标方程为
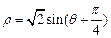
.
(Ⅰ)求曲线
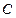
的直角坐标方程;
(Ⅱ)设直线
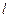
与曲线
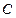
相交于
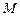
,
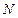
两点,求
M,N两点间的距离.
题号:1279705
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—1:几何证明选讲
如图,已知
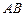
是
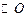
的直径,
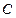
,
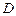
是
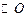
上两点,
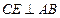
于
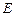
,
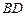
交
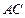
于
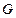
,交
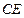
于
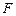
,
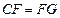
.
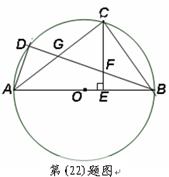
(Ⅰ)求证:
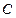
是
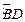
的中点;
(Ⅱ)求证:
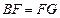
.
题号:1279906
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(本小题满分
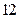
分)在平面直角坐标系中,已知两个定点
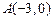
和
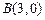
.动点
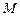
在
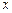
轴上的射影是
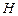
(
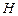
随
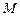
移动而移动),若对于每个动点
M总存在相应的点
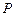
满足
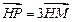
,且
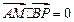
.
(Ⅰ)求动点
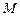
的轨迹
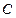
的方程;
(Ⅱ)设过定点
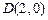
的直线
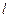
(直线
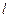
与
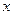
轴不重合)交曲线
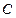
于
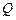
,
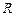
两点,求证:直线
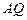
与直线
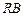
交点总在某直线
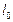
上.
题号:1279907
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(本小题满分
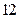
分)
在四棱锥
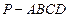
中,平面
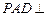
平面
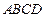
,△
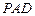
是等边三角形,底面
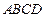
是边长为
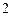
的菱形,
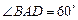
,
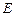
是
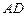
的中点,
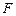
是
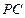
的中点.
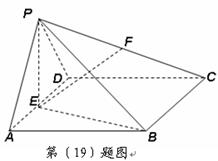
(Ⅰ)求证:
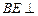
平面
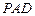
;
(Ⅱ) 求证:
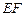
∥平面
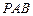
;
(Ⅲ) 求直线
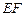
与平面
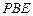
所成角的余弦值.
题号:1279908
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(本小题满分
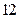
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为
A类同学),另外250名同学不经常参加体育锻炼(称为
B类同学),现用分层抽样方法(按
A类、
B类分二层)从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为
A类同学,乙为
B类同学;
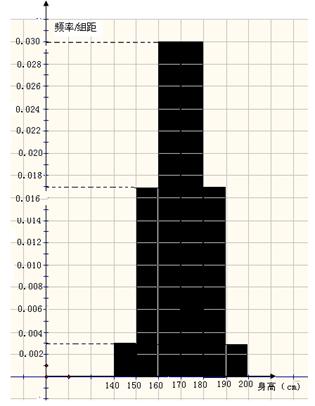
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间
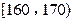
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
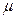
及标准差
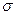
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在
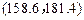
范围中的学生的人数.
(Ⅲ) 如果以身高达170
cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| 身高达标
| 身高不达标
| 总计
|
积极参加体育锻炼
| 40
|
|
|
不积极参加体育锻炼
|
| 15
|
|
总计
|
|
| 100
|
(ⅰ)完成上表;
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:
K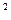
=
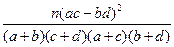
,参考数据:
P(K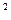 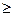 k) k)
| 0.40
| 0.25
| 0.15
| 0.10
| 0.05
| 0.025
|
k
| 0.708
| 1.323
| 2.072
| 2.706
| 3.841
| 5.024
|
题号:1279909
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(本小题满分
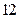
分)设数列
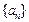
的前
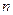
项和为
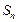
,且
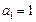
,
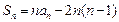
.
(Ⅰ)求
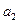
,
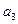
,
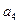
,并求出数列
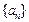
的通项公式;
(Ⅱ)设数列
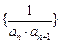
的前
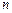
项和为
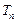
,试求
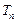
的取值范围.
题号:3877389
题型:解答题
难易度:容易
日期:2010-05-19
来源:2010年海南省海口市高考调研考试数学(理)
【题文】(本小题满分
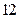
分)已知函数
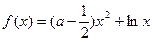
(
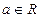
).
(Ⅰ)当
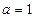
时,求
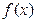
在区间[1,
e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数
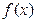
的图象恒在直线
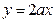
下方,求
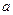
的取值范围.
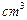 )为
)为
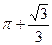
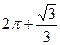
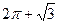
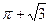
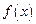 在
在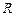 上满足
上满足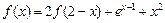 ,则曲线
,则曲线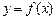 在点
在点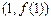 处的切线方程是
处的切线方程是 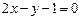
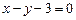
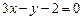
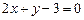
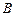 自由下落时,进入槽口
自由下落时,进入槽口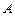 处的概率为
处的概率为 
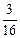
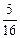
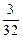
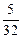
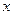 值是
值是
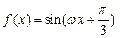 (
(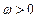 )的最小正周期为
)的最小正周期为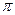 ,则该函数的图象
,则该函数的图象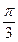 ,0)对称
,0)对称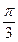 对称
对称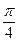 ,0)对称
,0)对称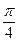 对称
对称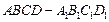 中,
中,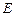 ,
,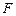 分别为
分别为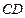 和
和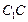 的中点,则直线
的中点,则直线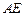 与
与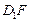 所成角的余弦值为
所成角的余弦值为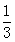
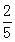
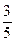
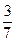
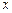 ,
,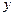 满足约束条件
满足约束条件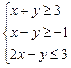 ,则目标函数
,则目标函数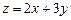 的最大值为
的最大值为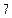
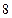
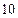
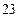

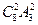
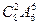
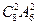
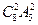
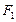 ,
,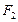 分别是双曲线
分别是双曲线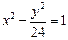 的左、右焦点,
的左、右焦点,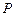 是双曲线上的一点,若
是双曲线上的一点,若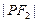 ,
,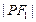 ,
,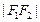 构成公差为正数的等差数列,则
构成公差为正数的等差数列,则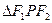 的面积为
的面积为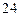
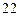
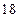
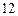
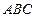 中,
中,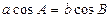 ,则△
,则△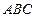 是
是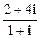 (
(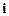 是虚数单位)的值是
是虚数单位)的值是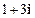
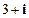
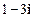
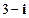
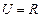 ,
,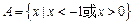 ,
,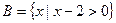 ,则
,则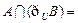
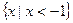
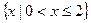
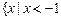 或
或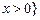
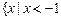 或
或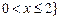
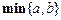 表示
表示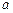 ,
,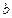 两个数中的最小值,设
两个数中的最小值,设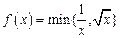 (
(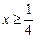 ),则由函数
),则由函数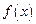 的图象,
的图象,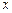 轴与直线
轴与直线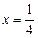 和直线
和直线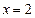 所围成的封闭图形的面积为_____
所围成的封闭图形的面积为_____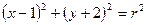 上有且只有两个点到直线
上有且只有两个点到直线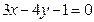 的距离等于1,则
的距离等于1,则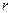 的取值范围是
的取值范围是 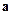 ,
,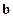 ,
,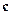 ,有下列四个命题:
,有下列四个命题: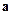 ∥
∥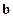 ,
,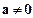 ,
,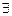
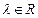 ,使得
,使得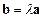 ;
;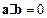 ,则
,则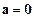 或
或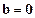 ;
;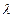 ,
,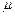 使得
使得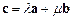 ;
;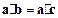 ,则
,则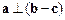 .
.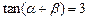 ,
,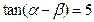 ,则
,则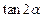 的值为_________.
的值为_________. 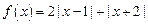 .
.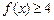 的解集;
的解集;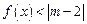 的解集是非空的集合,求实数
的解集是非空的集合,求实数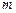 的取值范围.
的取值范围.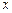 轴的正半轴重合.直线
轴的正半轴重合.直线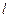 的参数方程是
的参数方程是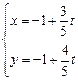 (
(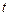 为参数),曲线
为参数),曲线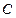 的极坐标方程为
的极坐标方程为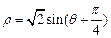 .
.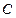 的直角坐标方程;
的直角坐标方程;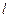 与曲线
与曲线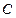 相交于
相交于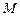 ,
,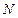 两点,求M,N两点间的距离.
两点,求M,N两点间的距离.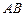 是
是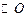 的直径,
的直径,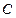 ,
,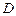 是
是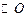 上两点,
上两点,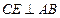 于
于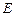 ,
,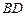 交
交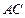 于
于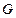 ,交
,交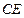 于
于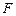 ,
,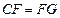 .
.
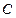 是
是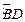 的中点;
的中点;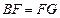 .
.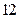 分)在平面直角坐标系中,已知两个定点
分)在平面直角坐标系中,已知两个定点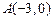 和
和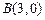 .动点
.动点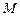 在
在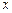 轴上的射影是
轴上的射影是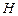 (
(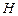 随
随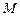 移动而移动),若对于每个动点M总存在相应的点
移动而移动),若对于每个动点M总存在相应的点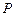 满足
满足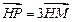 ,且
,且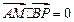 .
.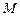 的轨迹
的轨迹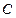 的方程;
的方程;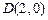 的直线
的直线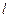 (直线
(直线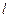 与
与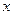 轴不重合)交曲线
轴不重合)交曲线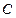 于
于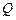 ,
,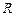 两点,求证:直线
两点,求证:直线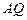 与直线
与直线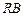 交点总在某直线
交点总在某直线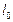 上.
上.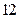 分)
分)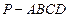 中,平面
中,平面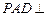 平面
平面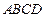 ,△
,△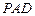 是等边三角形,底面
是等边三角形,底面 是边长为
是边长为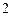 的菱形,
的菱形,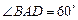 ,
,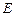 是
是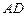 的中点,
的中点,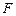 是
是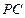 的中点.
的中点.
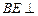 平面
平面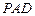 ;
;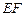 ∥平面
∥平面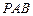 ;
;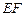 与平面
与平面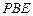 所成角的余弦值.
所成角的余弦值.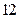 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
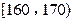 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望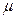 及标准差
及标准差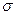 (精确到0.1);
(精确到0.1);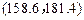 范围中的学生的人数.
范围中的学生的人数.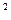 =
=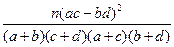 ,参考数据:
,参考数据: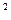
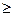 k)
k)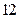 分)设数列
分)设数列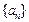 的前
的前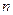 项和为
项和为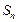 ,且
,且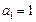 ,
,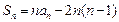 .
.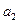 ,
,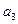 ,
,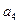 ,并求出数列
,并求出数列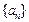 的通项公式;
的通项公式;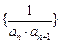 的前
的前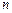 项和为
项和为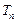 ,试求
,试求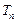 的取值范围.
的取值范围. 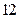 分)已知函数
分)已知函数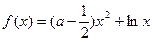 (
(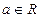 ).
).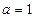 时,求
时,求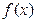 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;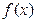 的图象恒在直线
的图象恒在直线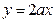 下方,求
下方,求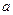 的取值范围.
的取值范围.