适用年级:{{getGradeNameByProperty('高三|高考模拟|湖南|2017年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|湖南|2017年')}} 使用省份:{{getAreaName('高三|高考模拟|湖南|2017年')}}
试卷年份:{{getYear('高三|高考模拟|湖南|2017年')}}上传日期:2017-04-16题数:10
提示:单击题文可显示答案与解析。
题号:846467
题型:选择题
难易度:较易
日期:2015-04-02
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
题号:3532704
题型:选择题
难易度:一般
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
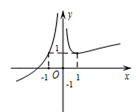
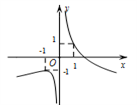
【题文】函数
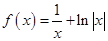
的图象大致为
题号:3532705
题型:选择题
难易度:一般
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
题号:3532706
题型:选择题
难易度:容易
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
题号:3532707
题型:选择题
难易度:容易
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
题号:3532708
题型:选择题
难易度:容易
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
题号:713737
题型:填空题
难易度:较难
日期:2016-09-18
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
【题文】设定义域为
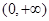
的单调函数
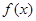
,对任意的
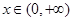
,都有
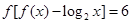
成立,若
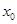
是方程
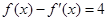
的一个解,且
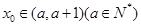
,则
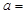
_______.
题号:3532701
题型:解答题
难易度:较难
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
【题文】已知函数
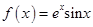
.
⑴求函数
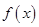
的单调区间;
⑵如果对于任意的

,
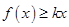
恒成立,求实数
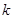
的取值范围;
⑶设函数
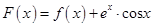
,

.过点
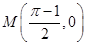
作函数
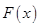
的图象
的所有切线,令各切点的横坐标构成数列
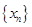
,求数列
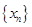
的所有项之和
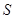
的值.
题号:3532702
题型:解答题
难易度:容易
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
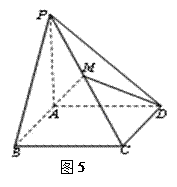
【题文】如图5所示,已知四棱锥
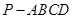
中,底面
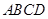
为矩形,
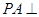
底面
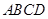
,
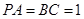
,
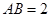
,

为
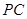
的中点.
⑴指出平面
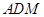
与
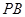
的交点

所在位置,并给出理由;
⑵求平面
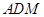
将四棱锥
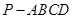
分成上下两部分的体积比.
题号:3532703
题型:解答题
难易度:容易
日期:2017-04-16
来源:湖南省张家界市2017届高中毕业班第二次联考数学文试题
【题文】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
| 喜欢甜品
| 不喜欢甜品
| 合 计
|
南方学生
| 60
| 20
| 80
|
北方学生
| 10
| 10
| 20
|
合 计
| 70
| 30
| 100
|
⑴根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差
异”;
⑵已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机
抽取3人,求至多有1人喜欢甜品的概率.
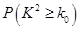
| 0.100
| 0.050
| 0.010
|
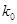
| 2.706
| 3.841
| 6.635
|
附:
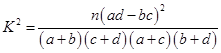
,
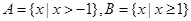 ,则“
,则“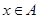 且
且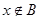 ”成立的充要条件是( )
”成立的充要条件是( )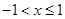
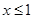
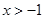
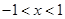
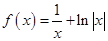 的图象大致为
的图象大致为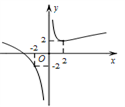
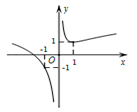
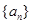 为等比数列,且
为等比数列,且 ,
, ,则
,则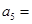
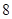

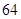

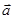 、
、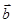 满足
满足 ,且
,且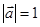 ,
,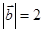 ,则
,则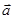 与
与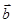 的夹角为
的夹角为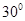
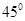
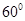
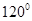
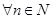 ,
,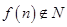 且
且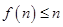 ”的否定形式是
”的否定形式是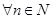 ,
,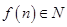 且
且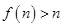
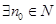 ,
,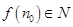 且
且
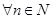 ,
,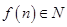 或
或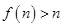
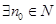 ,
,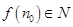 或
或
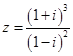 (其中
(其中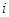 为虚数单位),则
为虚数单位),则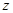 的虚部为
的虚部为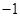
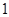
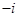
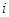
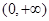 的单调函数
的单调函数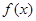 ,对任意的
,对任意的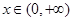 ,都有
,都有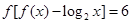 成立,若
成立,若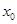 是方程
是方程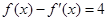 的一个解,且
的一个解,且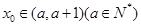 ,则
,则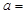 _______.
_______.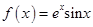 .
.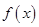 的单调区间;
的单调区间; ,
,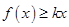 恒成立,求实数
恒成立,求实数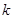 的取值范围;
的取值范围;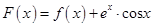 ,
, .过点
.过点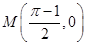 作函数
作函数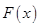 的图象
的图象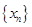 ,求数列
,求数列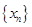 的所有项之和
的所有项之和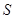 的值.
的值.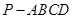 中,底面
中,底面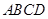 为矩形,
为矩形,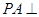 底面
底面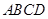 ,
,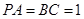 ,
,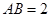 ,
, 为
为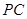 的中点.
的中点.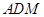 与
与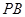 的交点
的交点 所在位置,并给出理由;
所在位置,并给出理由;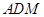 将四棱锥
将四棱锥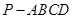 分成上下两部分的体积比.
分成上下两部分的体积比.
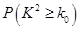
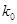
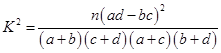 ,
,