适用年级:{{getGradeNameByProperty('高三|高考模拟|辽宁|2017年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|辽宁|2017年')}} 使用省份:{{getAreaName('高三|高考模拟|辽宁|2017年')}}
试卷年份:{{getYear('高三|高考模拟|辽宁|2017年')}}上传日期:2017-06-16题数:23
提示:单击题文可显示答案与解析。
题号:684112
题型:选择题
难易度:较易
日期:2016-12-19
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】阅读下边的程序框图,运行相应的程序,输出的结果为( )
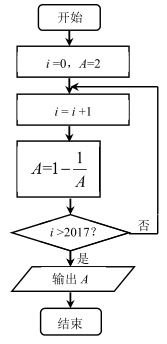
| A.-2 | B.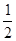 | C.-1 | D.2 |
题号:765575
题型:选择题
难易度:较易
日期:2016-03-21
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】下表提供了某厂节能降耗技术改造后在生产
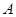
产品过程中记录的产量
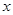
(吨)与相应的生产能耗
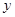
(吨)的几组对应数据,根据下表提供的数据,求出
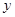
关于
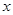
的线性回归方程为
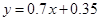
,则下列结论错误的是( )

A.线性回归直线一定过点 |
| B.产品的生产能耗与产量呈正相关 |
C.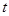 的取值为3.15 的取值为3.15 |
D.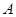 产品每多生产1吨,则相应的生产能耗约增加0.7吨 产品每多生产1吨,则相应的生产能耗约增加0.7吨 |
题号:3533270
题型:选择题
难易度:较易
日期:2017-04-13
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
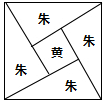
【题文】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用
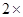
勾
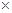
股
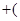
股
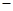
勾
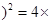
朱实
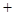
黄实
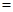
弦实,化简,得勾
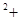
股
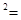
弦
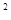
.设勾股形中勾股比为
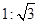
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
题号:3799381
题型:选择题
难易度:较难
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】设函数
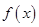
在
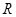
上存在导数
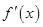
,
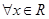
,有
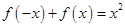
,在
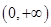
上
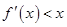
,若
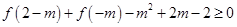
,则实数
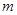
的取值范围为( )
题号:3799382
题型:选择题
难易度:一般
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】已知双曲线
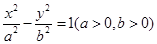
左右焦点分别为
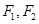
,渐近线为
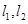
,
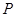
位于
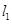
在第一象限内的部分,若
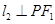
,
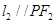
,则双曲线的离心率为( )
题号:3799383
题型:选择题
难易度:一般
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
题号:3799384
题型:选择题
难易度:一般
日期:2017-06-16
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】已知
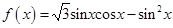
,把
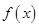
的图象向右平移
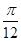
个单位,再向上平移2个单位,得到
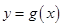
的图象,若对任意实数
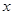
,都有
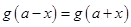
成立,则
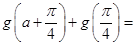
( )
| A.3 | B.4 | C.2 | D.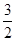 |
题号:3799385
题型:选择题
难易度:一般
日期:2017-06-16
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】设命题
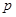
:实数
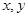
满足:
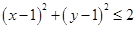
,命题
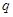
:实数
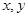
满足:
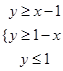
,则
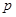
是
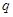
的( )条件
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
题号:3799386
题型:选择题
难易度:一般
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
题号:3799387
题型:选择题
难易度:一般
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
题号:3799388
题型:选择题
难易度:一般
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
题号:3899183
题型:选择题
难易度:一般
日期:2017-07-26
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,俯视图是圆心角为
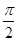
的扇形,则该几何体的侧面积为( )
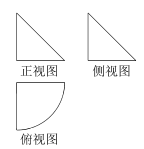
题号:3799377
题型:填空题
难易度:一般
日期:2017-06-16
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】将正整数12分解成两个正整数的乘积有
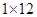
,
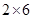
,
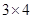
三种,其中
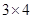
是这三种分解中两数差的绝对值最小的,我们称
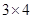
为12的最佳分解. 当
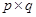
(
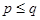
且
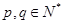
)是正整数
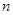
的最佳分解时,我们定义函数
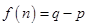
,例如
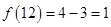
,数列
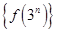
的前100项和为__________.
题号:3799378
题型:填空题
难易度:一般
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】三棱锥
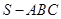
的所有顶点都在球
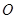
的球面上,
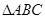
是边长为3的正三角形,
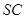
是球
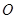
的直径,且
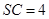
,则此三棱锥的体积
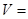
__________.
题号:3799379
题型:填空题
难易度:一般
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】设抛物线
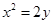
的焦点为
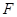
,经过点
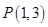
的直线
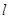
与抛物线相交于
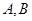
两点,且点
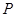
恰为
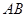
的中点,则
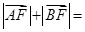
__________.
题号:3799380
题型:填空题
难易度:一般
日期:2017-06-16
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】
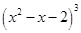
展开式中
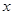
项的系数为__________.
题号:3434701
题型:解答题
难易度:一般
日期:2017-03-21
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】选修4-4:坐标系与参数方程
已知曲线
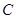
在平面直角坐标系
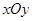
下的参数方程为
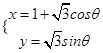
(
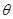
为参数),以坐标原点
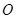
为极点,以
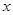
轴正半轴为极轴,建立极坐标系.
(1)求曲线
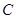
的普通方程及极坐标方程;
(2)直线
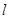
的极坐标方程是
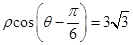
,射线

:
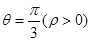
与曲线
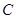
交于点
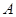
与直线
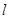
交于点
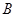
,求线段
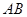
的长.
题号:3533246
题型:解答题
难易度:较易
日期:2017-04-13
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】选修4-5:不等式选讲
已知函数
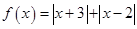
.
(Ⅰ)若
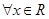
,
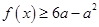
恒成立,求实数
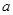
的取值范围;
(Ⅱ)求函数
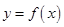
的图象与直线
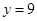
围成的封闭图形的面积.
题号:3533249
题型:解答题
难易度:一般
日期:2017-04-13
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】已知椭圆

:
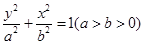
的上下两个焦点分别为
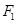
,
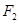
,过点
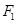
与
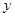
轴垂直的直线交椭圆

于
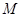
、
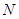
两点,
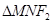
的面积为
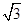
,椭圆

的离心力为
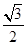
.
(Ⅰ)求椭圆

的标准方程;
(Ⅱ)已知
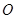
为坐标原点,直线
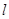
:
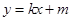
与
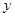
轴交于点
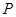
,与椭圆

交于
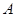
,
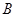
两个不同的点,若存在实数
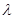
,使得
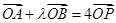
,求
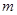
的取值范围.
题号:3799373
题型:解答题
难易度:困难
日期:2017-06-17
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】已知
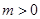
,设函数
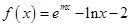
.
(1)若
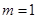
,证明:存在唯一实数
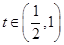
,使得
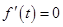
;
(2)若当
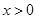
时,
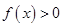
,证明:
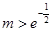
.
题号:3799374
题型:解答题
难易度:一般
日期:2017-06-16
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】在四棱锥
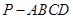
中,
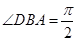
,
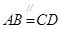
,
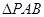
和
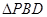
都是边长为2的等边三角形,设
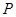
在底面
的射影为
.
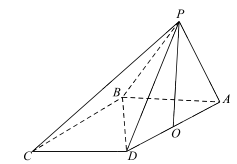
(1)证明:
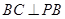
;
(2)求二面角
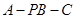
的余弦值.
题号:3799375
题型:解答题
难易度:一般
日期:2017-06-16
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布
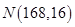
.现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组
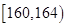
,第二组

,…,第六组
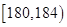
,如图是按上述分组方法得到的频率分布直方图.
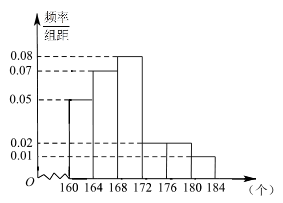
(1)试评估该社区被测试的50名市民的成绩在全市市民中成绩的平均状况及这50名市民成绩在172个以上(含172个)的人数;
(2)在这50名市民中成绩在172个以上(含172个)的人中任意抽取2人,该2人中成绩排名(从高到低)在全市前130名的人数记为
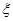
,求
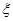
的数学期望.
参考数据:若
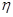
~
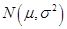
,则
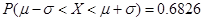
,
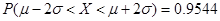
,
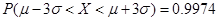
.
题号:3799376
题型:解答题
难易度:一般
日期:2017-06-16
来源:【全国市级联考】辽宁省锦州市2017届高三质量检测(一)数学(理)试题
【题文】已知函数
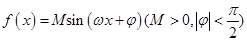
的部分图象如图所示.
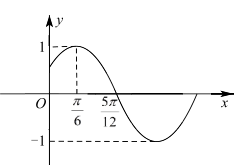
(1)求函数
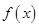
的解析式;
(2)在
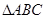
中,角

的对边分别是
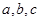
,若
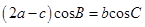
,求
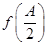
的取值范围.

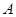 产品过程中记录的产量
产品过程中记录的产量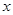 (吨)与相应的生产能耗
(吨)与相应的生产能耗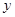 (吨)的几组对应数据,根据下表提供的数据,求出
(吨)的几组对应数据,根据下表提供的数据,求出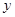 关于
关于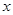 的线性回归方程为
的线性回归方程为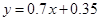 ,则下列结论错误的是( )
,则下列结论错误的是( )

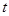 的取值为3.15
的取值为3.15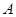 产品每多生产1吨,则相应的生产能耗约增加0.7吨
产品每多生产1吨,则相应的生产能耗约增加0.7吨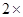 勾
勾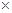 股
股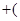 股
股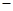 勾
勾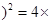 朱实
朱实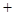 黄实
黄实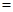 弦实,化简,得勾
弦实,化简,得勾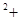 股
股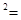 弦
弦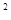 .设勾股形中勾股比为
.设勾股形中勾股比为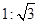 ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
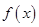 在
在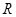 上存在导数
上存在导数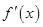 ,
,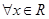 ,有
,有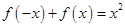 ,在
,在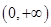 上
上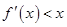 ,若
,若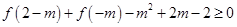 ,则实数
,则实数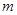 的取值范围为( )
的取值范围为( )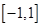
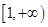
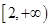
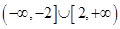
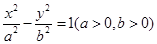 左右焦点分别为
左右焦点分别为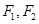 ,渐近线为
,渐近线为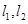 ,
,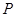 位于
位于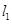 在第一象限内的部分,若
在第一象限内的部分,若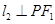 ,
,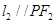 ,则双曲线的离心率为( )
,则双曲线的离心率为( )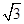
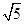
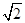
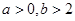 ,且
,且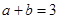 ,则
,则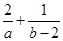 的最小值是( )
的最小值是( )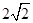
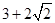
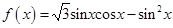 ,把
,把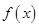 的图象向右平移
的图象向右平移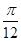 个单位,再向上平移2个单位,得到
个单位,再向上平移2个单位,得到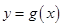 的图象,若对任意实数
的图象,若对任意实数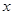 ,都有
,都有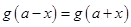 成立,则
成立,则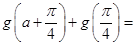 ( )
( )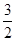
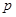 :实数
:实数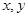 满足:
满足: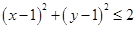 ,命题
,命题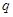 :实数
:实数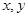 满足:
满足: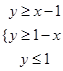 ,则
,则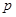 是
是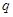 的( )条件
的( )条件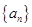 的前
的前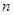 项和为
项和为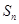 ,其中
,其中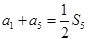 ,且
,且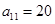 ,则
,则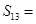 ( )
( )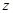 满足
满足 ,则
,则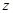 的虚部是( )
的虚部是( )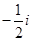
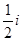
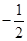
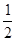
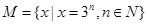 ,集合
,集合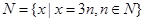 ,则集合
,则集合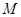 与集合
与集合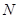 的关系( )
的关系( )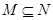
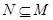

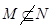 且
且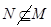
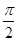 的扇形,则该几何体的侧面积为( )
的扇形,则该几何体的侧面积为( )
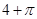
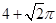

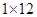 ,
,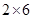 ,
,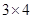 三种,其中
三种,其中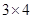 是这三种分解中两数差的绝对值最小的,我们称
是这三种分解中两数差的绝对值最小的,我们称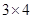 为12的最佳分解. 当
为12的最佳分解. 当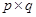 (
(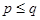 且
且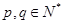 )是正整数
)是正整数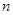 的最佳分解时,我们定义函数
的最佳分解时,我们定义函数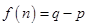 ,例如
,例如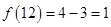 ,数列
,数列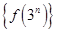 的前100项和为__________.
的前100项和为__________. 的所有顶点都在球
的所有顶点都在球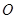 的球面上,
的球面上,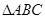 是边长为3的正三角形,
是边长为3的正三角形,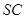 是球
是球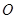 的直径,且
的直径,且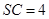 ,则此三棱锥的体积
,则此三棱锥的体积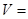 __________.
__________.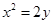 的焦点为
的焦点为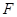 ,经过点
,经过点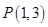 的直线
的直线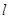 与抛物线相交于
与抛物线相交于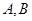 两点,且点
两点,且点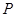 恰为
恰为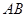 的中点,则
的中点,则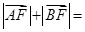 __________.
__________.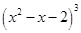 展开式中
展开式中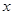 项的系数为__________.
项的系数为__________.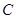 在平面直角坐标系
在平面直角坐标系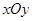 下的参数方程为
下的参数方程为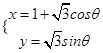 (
(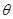 为参数),以坐标原点
为参数),以坐标原点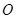 为极点,以
为极点,以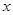 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.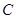 的普通方程及极坐标方程;
的普通方程及极坐标方程;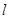 的极坐标方程是
的极坐标方程是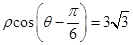 ,射线
,射线 :
: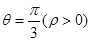 与曲线
与曲线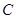 交于点
交于点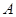 与直线
与直线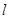 交于点
交于点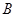 ,求线段
,求线段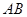 的长.
的长.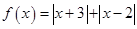 .
.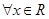 ,
,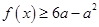 恒成立,求实数
恒成立,求实数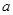 的取值范围;
的取值范围;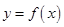 的图象与直线
的图象与直线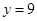 围成的封闭图形的面积.
围成的封闭图形的面积. :
: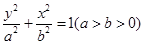 的上下两个焦点分别为
的上下两个焦点分别为 ,
, ,过点
,过点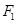 与
与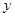 轴垂直的直线交椭圆
轴垂直的直线交椭圆 于
于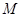 、
、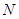 两点,
两点,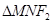 的面积为
的面积为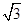 ,椭圆
,椭圆 的离心力为
的离心力为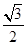 .
. 的标准方程;
的标准方程; 为坐标原点,直线
为坐标原点,直线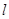 :
: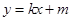 与
与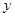 轴交于点
轴交于点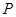 ,与椭圆
,与椭圆 交于
交于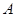 ,
,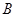 两个不同的点,若存在实数
两个不同的点,若存在实数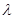 ,使得
,使得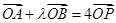 ,求
,求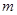 的取值范围.
的取值范围.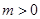 ,设函数
,设函数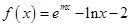 .
.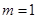 ,证明:存在唯一实数
,证明:存在唯一实数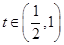 ,使得
,使得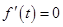 ;
;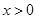 时,
时,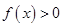 ,证明:
,证明: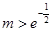 .
.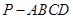 中,
中,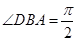 ,
,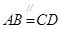 ,
,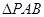 和
和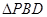 都是边长为2的等边三角形,设
都是边长为2的等边三角形,设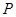 在底面
在底面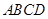 的射影为
的射影为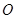 .
.
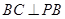 ;
;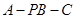 的余弦值.
的余弦值.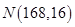 .现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组
.现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组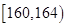 ,第二组
,第二组 ,…,第六组
,…,第六组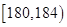 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
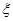 ,求
,求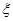 的数学期望.
的数学期望.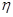 ~
~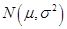 ,则
,则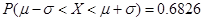 ,
,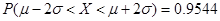 ,
,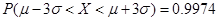 .
.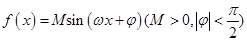 的部分图象如图所示.
的部分图象如图所示.
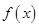 的解析式;
的解析式; 中,角
中,角 的对边分别是
的对边分别是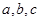 ,若
,若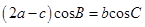 ,求
,求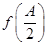 的取值范围.
的取值范围.