适用年级:{{getGradeNameByProperty('高三|高考模拟|广东|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|广东|2014年')}} 使用省份:{{getAreaName('高三|高考模拟|广东|2014年')}}
试卷年份:{{getYear('高三|高考模拟|广东|2014年')}}上传日期:2014-06-12题数:20
提示:单击题文可显示答案与解析。
题号:911169
题型:选择题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】对任意实数
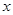
、
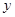
,定义运算
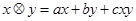
,其中
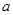
、
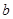
、
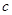
是常数,等式右边的运算
是通常的加法和乘法运算.已知
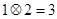
,
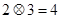
,并且有一个非零常数
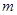
,使得
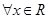
,都有
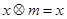
,则
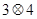
的值是( )
题号:911170
题型:选择题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】若变量
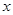
、
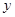
满足约束条件
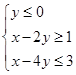
,则
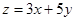
的取值范围是( )
题号:911171
题型:选择题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】已知平面
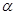
、
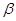
和直线
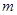
,给出条件:①
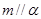
;②
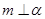
;③
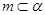
;④
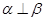
;⑤
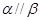
.
由这五个条件中的两个同时成立能推导出
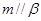
的是( )
题号:911192
题型:选择题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
题号:911193
题型:选择题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
题号:911194
题型:选择题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】已知等差数列
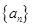
的前
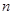
项和为
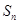
,且
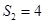
,
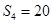
,则该数列的公差
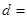
( )
题号:911195
题型:选择题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】若复数
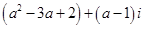
是纯虚数,则实数
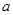
的值为( )
题号:911196
题型:选择题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
题号:911162
题型:填空题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
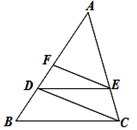
【题文】(几何证明选讲选做题)如图3,在
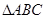
中,
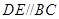
,
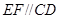
,若
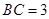
,
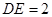
,
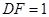
,则
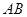
的长为_______.
题号:911163
题型:填空题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】(坐标系与参数方程选做题)在极坐标系中,直线
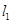
的方程是
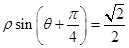
,以极点为原
点,以极轴为
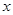
轴的正半轴建立直角坐标系,在直角坐标系中,直线
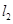
的方程是
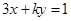
.如果直线
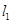
与
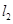
垂直,则常数
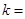
.
题号:911164
题型:填空题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】已知
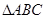
的内角
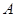
、
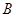
、
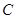
的对边分别为
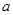
、
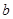
、
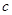
,且
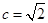
,
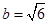
,
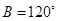
,则
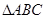
的面积等于________.
题号:911165
题型:填空题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】已知函数
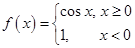
,则
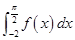
的值等于
.
题号:911166
题型:填空题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】执行如图的程序框图,输出的
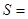
.

题号:911167
题型:填空题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】二项式
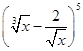
的展开式中常数项为_______.
题号:911168
题型:填空题
难易度:较易
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
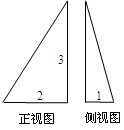
【题文】一个三棱锥的正视图和侧视图及其尺寸如图所示(均为直角三角形),则该三棱锥的俯视图的面积为
.
题号:911156
题型:解答题
难易度:较难
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】已知函数
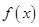
满足如下条件:当
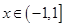
时,
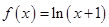
,且对任
意
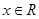
,都有

.
(1)求函数
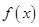
的图象在点
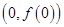
处的切线方程;
(2)求当
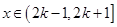
,
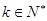
时,函数
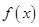
的解析式;
(3)是否存在
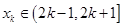
,
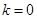
、
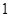
、

、
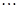
、
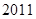
,使得等式
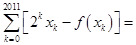
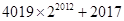
成立?若存在就求出
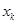
(
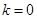
、
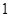
、

、
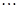
、
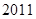
),若不存在,说明理由.
题号:911157
题型:解答题
难易度:较难
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】已知定点
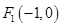
、
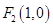
,动点
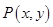
,且满足
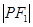
、
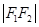
、
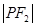
成等差数列.
(1)求点
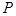
的轨迹
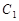
的方程;
(2)若曲线
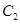
的方程为
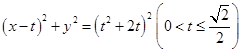
,过点
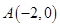
的直线
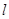
与曲线
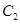
相切,
求直线
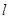
被曲线

截得的线段长的最小值.
题号:911158
题型:解答题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】设数
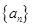
满足:
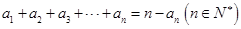
.
(1)求证:数列
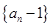
是等比数列;
(2)若
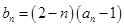
,且对任意的正整数
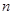
,都有
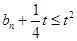
,求实数
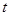
的取值范围.
题号:911160
题型:解答题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】地为绿化环境,移栽了银杏树

棵,梧桐树
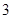
棵.它们移栽后的成活率分别
为
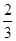
、
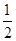
,每棵树是否存活互不影响,在移栽的
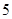
棵树中:
(1)求银杏树都成活且梧桐树成活

棵的概率;
(2)求成活的棵树
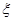
的分布列与期望.
题号:911161
题型:解答题
难易度:一般
日期:2014-06-12
来源:2014届广东省东莞市高三第二次模拟考试理科数学试卷(带解析)
【题文】设函数
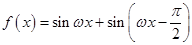
,
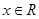
.
(1)若
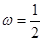
,求
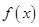
的最大值及相应的
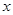
的取值集合;
(2)若
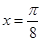
是
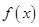
的一个零点,且
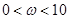
,求
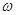
的值和
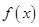
的最小正周期.
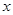 、
、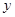 ,定义运算
,定义运算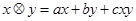 ,其中
,其中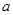 、
、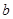 、
、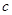 是常数,等式右边的运算
是常数,等式右边的运算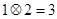 ,
,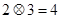 ,并且有一个非零常数
,并且有一个非零常数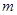 ,使得
,使得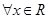 ,都有
,都有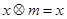 ,则
,则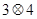 的值是( )
的值是( )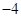
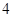
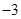
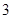
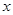 、
、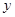 满足约束条件
满足约束条件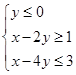 ,则
,则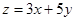 的取值范围是( )
的取值范围是( )
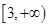
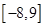
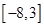
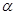 、
、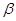 和直线
和直线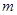 ,给出条件:①
,给出条件:①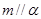 ;②
;②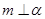 ;③
;③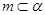 ;④
;④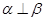 ;⑤
;⑤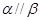 .
.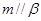 的是( )
的是( )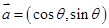 ,
,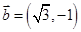 ,则
,则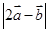 的最大值为( )
的最大值为( )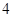
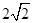

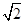
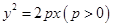 的准线与圆
的准线与圆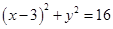 相切,则
相切,则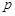 的值为( )
的值为( )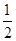
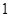

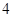
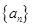 的前
的前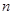 项和为
项和为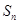 ,且
,且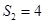 ,
,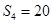 ,则该数列的公差
,则该数列的公差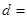 ( )
( )
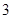
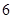
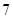
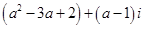 是纯虚数,则实数
是纯虚数,则实数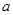 的值为( )
的值为( )
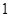
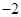
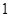 或
或
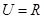 ,集合
,集合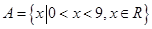 和
和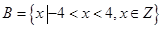 集合
集合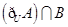 中
中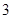 个
个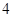 个
个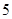 个
个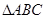 中,
中,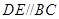 ,
,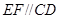 ,若
,若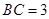 ,
,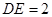 ,
,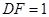 ,则
,则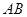 的长为_______.
的长为_______.
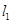 的方程是
的方程是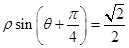 ,以极点为原
,以极点为原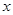 轴的正半轴建立直角坐标系,在直角坐标系中,直线
轴的正半轴建立直角坐标系,在直角坐标系中,直线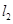 的方程是
的方程是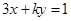 .如果直线
.如果直线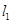 与
与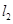
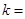 .
.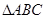 的内角
的内角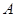 、
、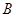 、
、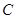 的对边分别为
的对边分别为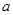 、
、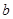 、
、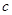 ,且
,且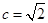 ,
,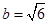 ,
,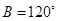 ,则
,则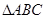 的面积等于________.
的面积等于________.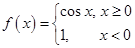 ,则
,则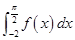 的值等于 .
的值等于 .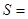 .
.
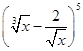 的展开式中常数项为_______.
的展开式中常数项为_______.
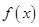 满足如下条件:当
满足如下条件:当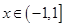 时,
时,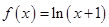 ,且对任
,且对任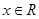 ,都有
,都有 .
.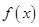 的图象在点
的图象在点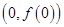 处的切线方程;
处的切线方程;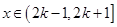 ,
,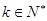 时,函数
时,函数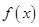 的解析式;
的解析式;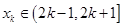 ,
,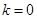 、
、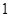 、
、 、
、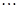 、
、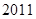 ,使得等式
,使得等式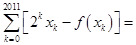
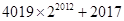 成立?若存在就求出
成立?若存在就求出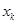 (
(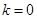 、
、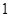 、
、 、
、 、
、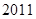 ),若不存在,说明理由.
),若不存在,说明理由.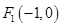 、
、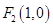 ,动点
,动点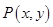 ,且满足
,且满足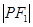 、
、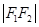 、
、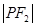
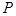 的轨迹
的轨迹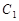 的方程;
的方程;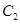 的方程为
的方程为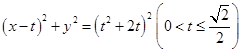 ,过点
,过点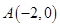 的直线
的直线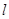 与曲线
与曲线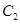 相切,
相切,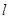 被曲线
被曲线 截得的线段长的最小值.
截得的线段长的最小值.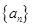 满足:
满足: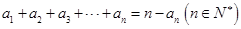 .
.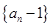 是等比数列;
是等比数列;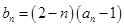 ,且对任意的正整数
,且对任意的正整数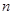 ,都有
,都有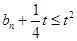 ,求实数
,求实数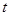 的取值范围.
的取值范围. 棵,梧桐树
棵,梧桐树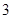 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别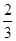 、
、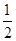 ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的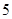 棵树中:
棵树中: 棵的概率;
棵的概率;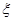 的分布列与期望.
的分布列与期望.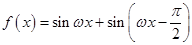 ,
,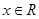 .
.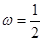 ,求
,求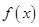 的最大值及相应的
的最大值及相应的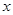 的取值集合;
的取值集合;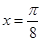 是
是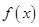 的一个零点,且
的一个零点,且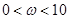 ,求
,求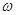 的值和
的值和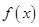 的最小正周期.
的最小正周期.