适用年级:{{getGradeNameByProperty('高三|高考模拟|北京|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|北京|2014年')}} 使用省份:{{getAreaName('高三|高考模拟|北京|2014年')}}
试卷年份:{{getYear('高三|高考模拟|北京|2014年')}}上传日期:2014-04-24题数:20
提示:单击题文可显示答案与解析。
题号:931176
题型:选择题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】直线
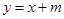
与圆
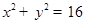
交于不同的两点
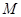
,
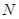
,且
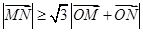
,其中
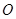
是坐标原点,则实数
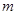
的取值范围是( )
题号:931177
题型:选择题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】已知函数
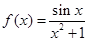
.下列命题:( )
①函数
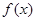
的图象关于原点对称; ②函数
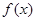
是周期函数;
③当
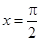
时,函数
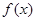
取最大值;④函数
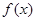
的图象与函数
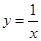
的图象没有公共点,其中正确命题的序号是
题号:931178
题型:选择题
难易度:容易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】执行如图所示的程序框图,输出的S值为( )
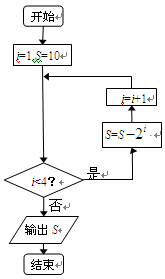
题号:931179
题型:选择题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】在
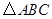
中,
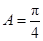
,
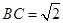
,则“
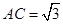
”是“
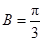
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
题号:931180
题型:选择题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
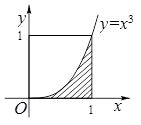
【题文】如图,设区域
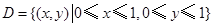
,向区域
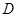
内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域
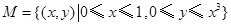
的概率为( )
题号:931181
题型:选择题
难易度:较易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
题号:931182
题型:选择题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
题号:931183
题型:选择题
难易度:较易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】复数
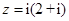
在复平面内对应的点位于 ( )
题号:931150
题型:填空题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
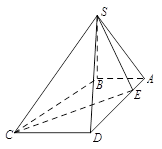
【题文】如图,在四棱锥
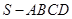
中,
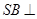
底面
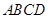
.底面
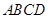
为梯形,
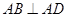
,
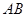
∥
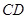
,
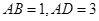
,
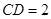
.若点
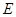
是线段
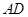
上的动点,则满足
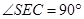
的点
的个数是
.
题号:931151
题型:填空题
难易度:较易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】有标号分别为1,2,3的红色卡片3张,标号分别为1,2,3的蓝色卡片3张,现将全部的6张卡片放在2行3列的格内(如图).若颜色相同的卡片在同一行,则不同的放法种数为
.(用数字作答)

题号:931172
题型:填空题
难易度:较易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】双曲线
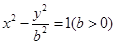
的一个焦点到其渐近线的距离是
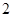
,则
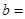
;此双曲线的离心率为
.
题号:931173
题型:填空题
难易度:较易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】某三棱锥的三视图如图所示,则这个三棱锥的体积为
;表面积为
.

题号:931174
题型:填空题
难易度:较易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】在极坐标系中,
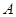
为曲线
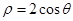
上的点,
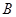
为曲线
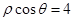
上的点,则线段
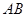
长度的最小值是
.
题号:931175
题型:填空题
难易度:较易
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】在各项均为正数的等比数列
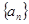
中,
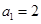
,
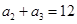
,则该数列的前4项和为
.
题号:931145
题型:解答题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】从
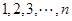
中这
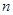
个数中取
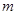
(
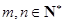
,
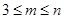
)个数组成递增等差数列,所有可能的递增等差数列的个数记为
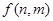
.
(1)当
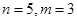
时,写出所有可能的递增等差数列及
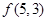
的值;
(2)求
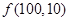
;
(3)求证:
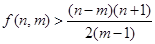
.
题号:931146
题型:解答题
难易度:较难
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】已知椭圆
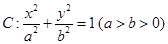
经过点
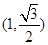
,离心率为
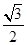
.
(1)求椭圆
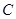
的方程;
(2)直线
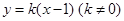
与椭圆
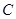
交于
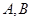
两点,点
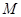
是椭圆
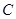
的右顶点.直线
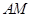
与直线
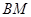
分别与
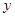
轴交于点
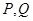
,试问以线段
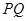
为直径的圆是否过
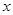
轴上的定点?若是,求出定点坐标;若不是,说明理由.
题号:931147
题型:解答题
难易度:较难
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】已知函数
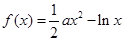
,
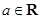
.
(1)求函数
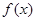
的单调区间;
(2)若函数
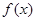
在区间
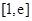
的最小值为
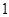
,求
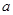
的值.
题号:931148
题型:解答题
难易度:较难
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】如图,四棱锥
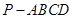
的底面为正方形,侧面
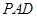
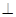
底面
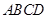
.
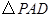
为等腰直角三角形,且
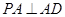
.
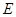
,
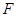
分别为底边
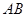
和侧棱
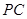
的中点.
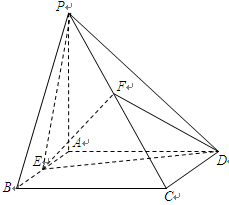
(1)求证:
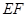
∥平面
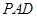
;
(2)求证:
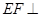
平面
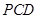
;
(3)求二面角
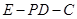
的余弦值.
题号:931149
题型:解答题
难易度:一般
日期:2014-04-24
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】已知函数
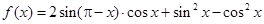
,
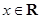
.
(1)求
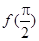
的值及函数
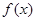
的最小正周期;
(2)求函数
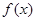
在
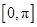
上的单调减区间.
题号:3496237
题型:解答题
难易度:一般
日期:2014-04-29
来源:2014届北京市朝阳区高三第一次综合练习理科数学试卷(带解析)
【题文】某单位从一所学校招收某类特殊人才.对
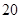
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:

例如,表中运动协调能力良好且逻辑思维能力一般的学生有
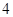
人.由于部分数据丢失,只知道从这
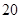
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
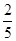
.
(1)求
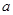
,
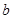
的值;
(2)从参加测试的
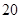
位学生中任意抽取
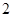
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(3)从参加测试的
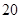
位学生中任意抽取
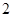
位,设运动协调能力或逻辑思维能力优秀的学生人数为
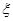
,求随机变量
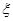
的分布列及其数学期望
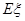
.
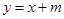 与圆
与圆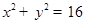 交于不同的两点
交于不同的两点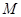 ,
,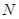 ,且
,且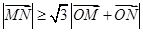 ,其中
,其中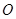 是坐标原点,则实数
是坐标原点,则实数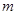 的取值范围是( )
的取值范围是( )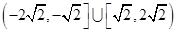
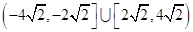
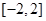
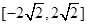
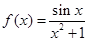 .下列命题:( )
.下列命题:( )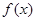 的图象关于原点对称; ②函数
的图象关于原点对称; ②函数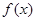 是周期函数;
是周期函数;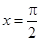 时,函数
时,函数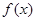 取最大值;④函数
取最大值;④函数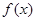 的图象与函数
的图象与函数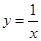 的图象没有公共点,其中正确命题的序号是
的图象没有公共点,其中正确命题的序号是
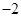
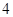
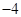
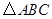 中,
中,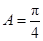 ,
,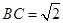 ,则“
,则“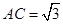 ”是“
”是“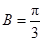 ”的( )
”的( )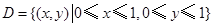 ,向区域
,向区域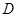 内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域
内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域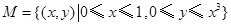 的概率为( )
的概率为( )
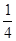
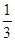
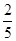
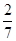
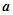 ,
,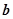 满足
满足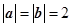 ,
,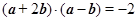 ,则
,则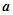 与
与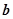 的夹角为( )
的夹角为( )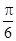
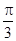
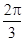
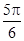
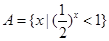 ,集合
,集合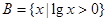 ,则
,则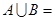 ( )
( )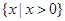
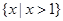
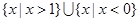
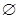
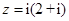 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( ) 中,
中, 底面
底面 .底面
.底面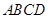 为梯形,
为梯形,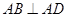 ,
, ∥
∥ ,
,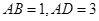 ,
,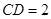 .若点
.若点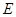 是线段
是线段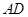 上的动点,则满足
上的动点,则满足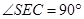 的点
的点 的个数是 .
的个数是 .

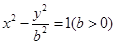 的一个焦点到其渐近线的距离是
的一个焦点到其渐近线的距离是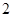 ,则
,则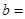 ;此双曲线的离心率为 .
;此双曲线的离心率为 .
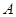 为曲线
为曲线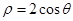 上的点,
上的点,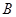 为曲线
为曲线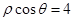 上的点,则线段
上的点,则线段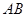 长度的最小值是 .
长度的最小值是 .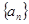 中,
中,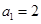 ,
,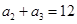 ,则该数列的前4项和为 .
,则该数列的前4项和为 .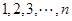 中这
中这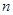 个数中取
个数中取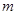 (
(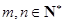 ,
,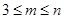 )个数组成递增等差数列,所有可能的递增等差数列的个数记为
)个数组成递增等差数列,所有可能的递增等差数列的个数记为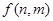 .
.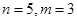 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及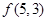 的值;
的值;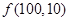 ;
;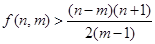 .
.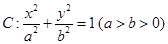 经过点
经过点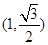 ,离心率为
,离心率为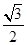 .
.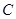 的方程;
的方程;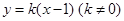 与椭圆
与椭圆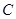 交于
交于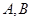 两点,点
两点,点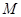 是椭圆
是椭圆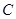 的右顶点.直线
的右顶点.直线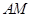 与直线
与直线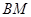 分别与
分别与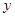 轴交于点
轴交于点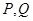 ,试问以线段
,试问以线段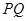 为直径的圆是否过
为直径的圆是否过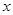 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.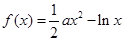 ,
,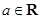 .
.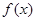 的单调区间;
的单调区间;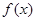 在区间
在区间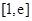 的最小值为
的最小值为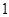 ,求
,求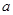 的值.
的值.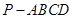 的底面为正方形,侧面
的底面为正方形,侧面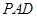
 底面
底面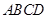 .
.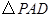 为等腰直角三角形,且
为等腰直角三角形,且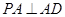 .
.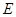 ,
,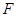 分别为底边
分别为底边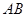 和侧棱
和侧棱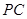 的中点.
的中点.
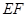 ∥平面
∥平面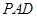 ;
;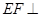 平面
平面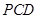 ;
; 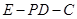 的余弦值.
的余弦值.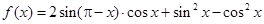 ,
,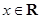 .
.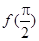 的值及函数
的值及函数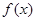 的最小正周期;
的最小正周期;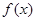 在
在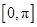 上的单调减区间.
上的单调减区间. 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
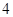 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这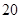 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为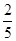 .
.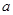 ,
,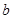 的值;
的值;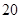 位学生中任意抽取
位学生中任意抽取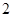 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;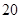 位学生中任意抽取
位学生中任意抽取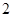 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为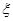 ,求随机变量
,求随机变量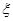 的分布列及其数学期望
的分布列及其数学期望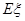 .
.