适用年级:{{getGradeNameByProperty('高三|高考模拟|北京|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|北京|2014年')}} 使用省份:{{getAreaName('高三|高考模拟|北京|2014年')}}
试卷年份:{{getYear('高三|高考模拟|北京|2014年')}}上传日期:2014-04-23题数:20
提示:单击题文可显示答案与解析。
题号:932344
题型:选择题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】已知动点

在椭圆
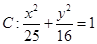
上,
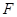
为椭圆

的右焦点,若点

满足
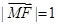
且
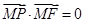
,则
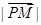
的最小值为( )
题号:932345
题型:选择题
难易度:容易
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】阅读右面的程序框图,运行相应的程序,输出的结果为( )
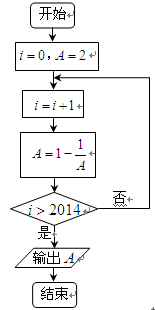
题号:932346
题型:选择题
难易度:容易
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】右图是某个三棱锥的三视图,其中主视图是等边三角形,左视图是直角三角形,俯视图是等腰直角三角形,则该三棱锥的体积是( )
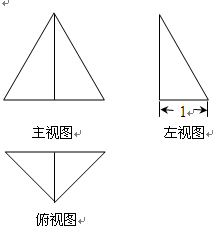
题号:932347
题型:选择题
难易度:容易
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】在平面直角坐标系
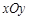
中,抛物线

上纵坐标为

的点到焦点的距离
为
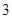
,则焦点到准线的距离为( )
题号:932348
题型:选择题
难易度:容易
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】已知
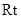
△

中,

以
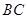
为直径的圆交

于
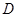
,则
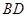
的长为( )

题号:932349
题型:选择题
难易度:容易
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】在

的展开式中,

的系数为( )
题号:932350
题型:选择题
难易度:容易
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
题号:3459373
题型:选择题
难易度:容易
日期:2014-04-25
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】下列函数中,在

内单调递减,并且是偶函数的是( )
题号:932338
题型:填空题
难易度:较难
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】若存在实常数
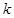
和
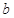
,使得函数

和
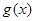
对其定义域上的任意实数
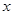
分别满足:

和

,则称直线
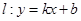
为

和
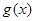
的“隔离直线”.已知函数
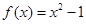
和函数
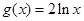
,那么函数

和函数
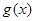
的隔离直线方程为_________.
题号:932339
题型:填空题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】各大学在高考录取时采取专业志愿优先的录取原则.一考生从某大学所给的
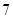
个专业中,选择
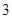
个作为自己的第一、二、三专业志愿,其中甲、乙两个专业不能同时兼报,则该考生有_____________种不同的填报专业志愿的方法(用数字作答).
题号:932340
题型:填空题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】已知变量
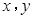
满足约束条件

则
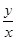
的取值范围是_________.
题号:932341
题型:填空题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】已知圆

的极坐标方程为
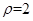
,以极点为原点,极轴为
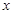
轴的正半轴建立平面直角坐标系,则圆

的直角坐标方程为_______________,若直线
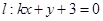
与圆

相切,则实数
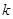
的值为_____________.
题号:932342
题型:填空题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】在等比数列
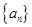
中,

,则数列
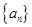
的通项公式
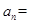
_____________,设

,则数列
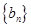
的前
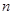
项和

_____________.
题号:932343
题型:填空题
难易度:容易
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】已知命题

:
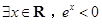
,则
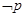
是____________________.
题号:932332
题型:解答题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】对于数列
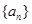
,把
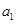
作为新数列
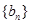
的第一项,把

或
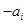
(
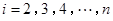
)作为新数列
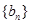
的第
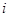
项,数列
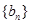
称为数列
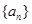
的一个生成数列.例如,数列
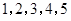
的一个生成数列是
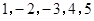
.已知数列
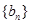
为数列
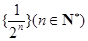
的生成数列,
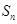
为数列
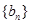
的前
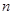
项和.
(1)写出
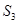
的所有可能值;
(2)若生成数列
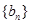
满足
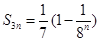
,求数列
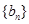
的通项公式;
(3)证明:对于给定的
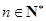
,

的所有可能值组成的集合为
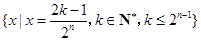
.
题号:932333
题型:解答题
难易度:较难
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】给定椭圆
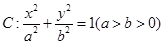
,称圆心在原点
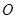
,半径为
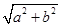
的圆是椭圆
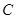
的“准圆”.若椭圆
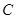
的一个焦点为

,其短轴上的一个端点到
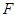
的距离为
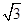
.
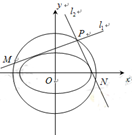
(1)求椭圆
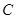
的方程和其“准圆”方程;
(2)点
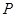
是椭圆
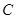
的“准圆”上的动点,过点
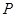
作椭圆的切线
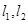
交“准圆”于点
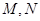
.
①当点
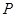
为“准圆”与
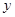
轴正半轴的交点时,求直线
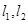
的方程并证明
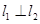
;
②求证:线段
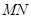
的长为定值.
题号:932334
题型:解答题
难易度:较难
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】设函数
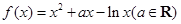
.
(1)若
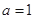
,求函数
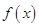
的单调区间;
(2)若函数

在区间
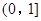
上是减函数,求实数
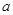
的取值范围;
(3)过坐标原点

作曲线
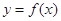
的切线,证明:切点的横坐标为

.
题号:932335
题型:解答题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】如图,正三棱柱
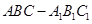
的底面边长是
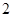
,侧棱长是
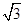
,
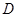
是
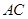
的中点.
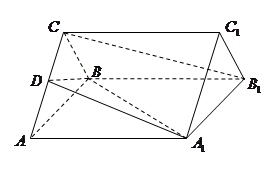
(1)求证:

∥平面

;
(2)求二面角

的大小;
(3)在线段
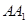
上是否存在一点
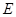
,使得平面
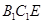
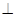
平面

,若存在,求出
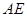
的长;若不存在,说明理由.
题号:932336
题型:解答题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出
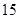
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
《中华人民共和国环境保护法》规定食品的汞含量不得超过
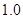
ppm.
(1)检查人员从这
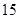
条鱼中,随机抽出
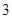
条,求
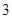
条中恰有

条汞含量超标的概率;
(2)若从这批数量很大的鱼中任选
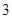
条鱼,记
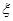
表示抽到的汞含量超标的鱼的条数.以此
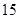
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
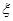
的分布列及数学期望
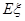
.
题号:932337
题型:解答题
难易度:一般
日期:2014-04-23
来源:2014届北京市石景山区高三一模理科数学试卷(带解析)
【题文】在△

中,角
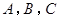
的对边分别为
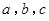
,且

,
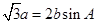
.
(1)求角
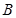
的大小;
(2)若
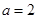
,
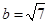
,求
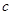
边的长和△

的面积.
 在椭圆
在椭圆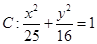 上,
上,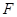 为椭圆
为椭圆 的右焦点,若点
的右焦点,若点 满足
满足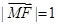 且
且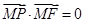 ,则
,则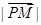 的最小值为( )
的最小值为( )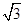
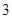
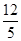


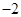
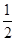
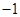
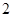

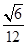
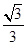
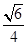
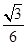
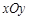 中,抛物线
中,抛物线 上纵坐标为
上纵坐标为 的点到焦点的距离
的点到焦点的距离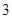 ,则焦点到准线的距离为( )
,则焦点到准线的距离为( )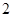

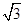
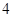
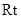 △
△ 中,
中, 以
以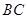 为直径的圆交
为直径的圆交 于
于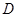 ,则
,则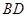 的长为( )
的长为( )
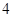
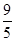
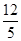
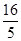
 的展开式中,
的展开式中, 的系数为( )
的系数为( )
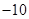
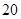

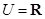 ,集合
,集合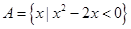 ,
,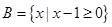 ,那么
,那么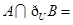 ( )
( )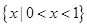
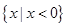
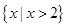
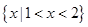
 内单调递减,并且是偶函数的是( )
内单调递减,并且是偶函数的是( )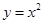
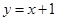
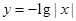
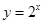
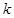 和
和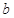 ,使得函数
,使得函数 和
和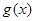 对其定义域上的任意实数
对其定义域上的任意实数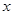 分别满足:
分别满足: 和
和 ,则称直线
,则称直线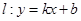 为
为 和
和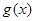 的“隔离直线”.已知函数
的“隔离直线”.已知函数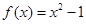 和函数
和函数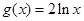 ,那么函数
,那么函数 和函数
和函数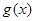 的隔离直线方程为_________.
的隔离直线方程为_________.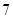 个专业中,选择
个专业中,选择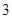 个作为自己的第一、二、三专业志愿,其中甲、乙两个专业不能同时兼报,则该考生有_____________种不同的填报专业志愿的方法(用数字作答).
个作为自己的第一、二、三专业志愿,其中甲、乙两个专业不能同时兼报,则该考生有_____________种不同的填报专业志愿的方法(用数字作答).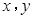 满足约束条件
满足约束条件 则
则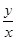 的取值范围是_________.
的取值范围是_________. 的极坐标方程为
的极坐标方程为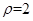 ,以极点为原点,极轴为
,以极点为原点,极轴为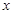 轴的正半轴建立平面直角坐标系,则圆
轴的正半轴建立平面直角坐标系,则圆 的直角坐标方程为_______________,若直线
的直角坐标方程为_______________,若直线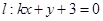 与圆
与圆 相切,则实数
相切,则实数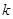 的值为_____________.
的值为_____________.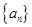 中,
中, ,则数列
,则数列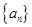 的通项公式
的通项公式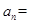 _____________,设
_____________,设 ,则数列
,则数列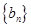 的前
的前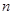 项和
项和 _____________.
_____________. :
: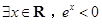 ,则
,则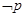 是____________________.
是____________________.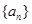 ,把
,把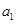 作为新数列
作为新数列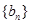 的第一项,把
的第一项,把 或
或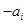 (
(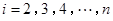 )作为新数列
)作为新数列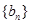 的第
的第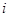 项,数列
项,数列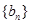 称为数列
称为数列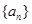 的一个生成数列.例如,数列
的一个生成数列.例如,数列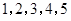 的一个生成数列是
的一个生成数列是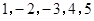 .已知数列
.已知数列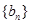 为数列
为数列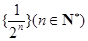 的生成数列,
的生成数列,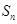 为数列
为数列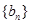 的前
的前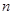 项和.
项和.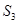 的所有可能值;
的所有可能值;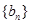 满足
满足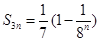 ,求数列
,求数列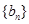 的通项公式;
的通项公式;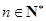 ,
, 的所有可能值组成的集合为
的所有可能值组成的集合为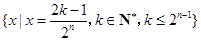 .
.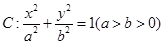 ,称圆心在原点
,称圆心在原点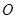 ,半径为
,半径为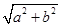 的圆是椭圆
的圆是椭圆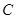 的“准圆”.若椭圆
的“准圆”.若椭圆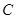 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到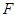 的距离为
的距离为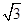 .
.
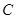 的方程和其“准圆”方程;
的方程和其“准圆”方程;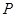 是椭圆
是椭圆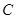 的“准圆”上的动点,过点
的“准圆”上的动点,过点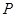 作椭圆的切线
作椭圆的切线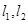 交“准圆”于点
交“准圆”于点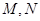 .
.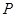 为“准圆”与
为“准圆”与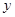 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线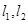 的方程并证明
的方程并证明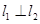 ;
;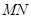 的长为定值.
的长为定值.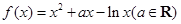 .
.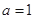 ,求函数
,求函数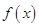 的单调区间;
的单调区间; 在区间
在区间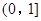 上是减函数,求实数
上是减函数,求实数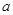 的取值范围;
的取值范围; 作曲线
作曲线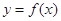 的切线,证明:切点的横坐标为
的切线,证明:切点的横坐标为 .
.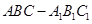 的底面边长是
的底面边长是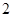 ,侧棱长是
,侧棱长是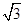 ,
,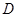 是
是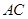 的中点.
的中点.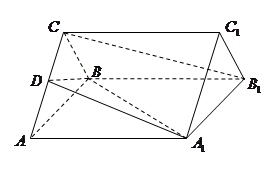
 ∥平面
∥平面 ;
; 的大小;
的大小;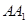 上是否存在一点
上是否存在一点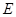 ,使得平面
,使得平面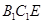
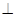 平面
平面 ,若存在,求出
,若存在,求出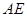 的长;若不存在,说明理由.
的长;若不存在,说明理由.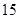 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
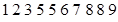
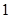
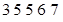
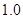 ppm.
ppm.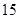 条鱼中,随机抽出
条鱼中,随机抽出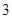 条,求
条,求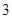 条中恰有
条中恰有 条汞含量超标的概率;
条汞含量超标的概率;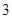 条鱼,记
条鱼,记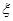 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此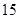 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求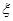 的分布列及数学期望
的分布列及数学期望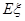 .
. 中,角
中,角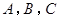 的对边分别为
的对边分别为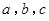 ,且
,且 ,
,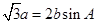 .
.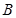 的大小;
的大小;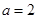 ,
,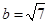 ,求
,求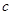 边的长和△
边的长和△ 的面积.
的面积.