适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-16题数:17
提示:单击题文可显示答案与解析。
题号:948720
题型:选择题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知数列{
an}的通项公式是
an=-
n2+12
n-32,其前
n项和是
Sn,对任意的
m,
n∈N
*且
m<
n,则
Sn-
Sm的最大值是( ).
题号:948721
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】
Sn是等比数列{
an}的前
n项和,
a1=
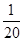
,9
S3=
S6,设
Tn=
a1a2a3…
an,则使
Tn取最小值的
n值为( ).
题号:948722
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知实数
a,
b,
c,
d成等比数列,且函数
y=ln(
x+2)-
x,当
x=
b时取到极大值
c,则
ad等于( ).
题号:948723
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】若-9,
a,-1成等差数列,-9,
m,
b,
n,-1成等比数列,则
ab=( ).
题号:948724
题型:选择题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】设{
an}是公差不为0的等差数列,
a1=2且
a1,
a3,
a6成等比数列,则{
an} 的前
n项和
Sn=( ).
题号:948725
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】在等差数列{
an}中,
a8=
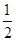 a11
a11+6,则数列{
an}前9项的和
S9等于( ).
题号:948726
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】若{
an}为等差数列,
Sn是其前
n项的和,且
S11=
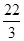
π,则tan
a6=( ).
题号:948727
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】公比为2的等比数列{
an}的各项都是正数,且
a3a11=16,则
a5=( ).
题号:946293
题型:填空题
难易度:较难
日期:2014-03-26
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知数列{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=3,b1=1,a2=b2,3a5=b3,若存在常数u,v对任意正整数n都有an=3logubn+v,则u+v=________.
题号:946296
题型:填空题
难易度:较易
日期:2014-03-26
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】设y=f(x)是一次函数,f(0)=1,且f(1),f(4),f(13)成等比数列,则f(2)+f(4)+…+f(2n)=________.
题号:946301
题型:填空题
难易度:容易
日期:2014-03-26
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】等差数列{an}前9项的和等于前4项的和.若a1=1,ak+a4=0,则k=________.
题号:946302
题型:填空题
难易度:较易
日期:2014-03-26
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】设公比为q(q>0)的等比数列{an}的前n项和为Sn,若S2=3a2+2,S4=3a4+2,则q=________.
题号:948713
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知数列{
an}的前
n项和为
Sn,且满足
Sn=
n2,数列{
bn}满足
bn=
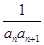
,
Tn为数列{
bn}的前
n项和.
(1)求数列{
an}的通项公式
an和
Tn;
(2)若对任意的
n∈N
*,不等式
λTn<
n+(-1)
n恒成立,求实数
λ的取值范围.
题号:948714
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知函数
f(
x)=
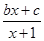
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数
f(
x)的解析式;
(2)若数列{
an}满足
a1=2,
an+1=
f(
an),试证明数列
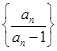
为等比数列,并求出数列{
an}的通项公式.
题号:948715
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知等差数列{an}满足:a2=5,a4+a6=22,数列{bn}满足b1+2b2+…
+2n-1bn=nan,设数列{bn}的前n项和为Sn.
(1)求数列{an},{bn}的通项公式;
(2)求满足13<Sn<14的n的集合.
题号:948716
题型:解答题
难易度:困难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知数列{
an}的前
n项和是
Sn,且
Sn+
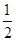 an
an=1.
(1)求数列{
an}的通项公式;
(2)记
bn=log
3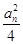
,数列
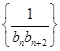
的前
n项和为
Tn,证明:
Tn<
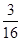
.
题号:4187800
题型:解答题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(带解析)
【题文】已知数列{
an}和{
bn}满足:
a1=
λ,
an+1=
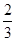 an
an+
n-4,
bn=(-1)
n(
an-3
n+21),其中
λ为实数,
n为正整数.
(1)对任意实数
λ,证明:数列{
an}不是等比数列;
(2)试判断数列{
bn}是否为等比数列,并证明你的结论.
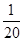 ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).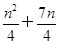
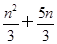
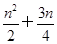
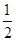 a11+6,则数列{an}前9项的和S9等于( ).
a11+6,则数列{an}前9项的和S9等于( ).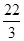 π,则tan a6=( ).
π,则tan a6=( ).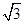
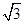
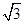
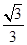
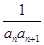 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.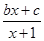 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.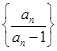 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.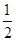 an=1.
an=1.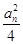 ,数列
,数列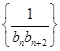 的前n项和为Tn,证明:Tn<
的前n项和为Tn,证明:Tn<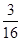 .
.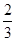 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.