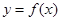 在
在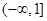 上有定义,对于给定的实数
上有定义,对于给定的实数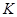 ,定义
,定义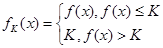 ,
,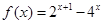 ,若对于任意
,若对于任意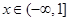 ,恒有
,恒有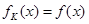 ,则( ).
,则( ).A.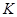 的最大值为 的最大值为 | B.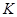 的最小值为 的最小值为 |
C.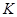 的最大值为 的最大值为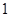 | D.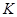 的最小值为 的最小值为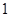 |
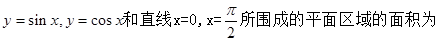 ( )
( )A.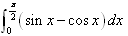 | B.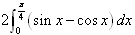 |
C.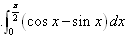 | D.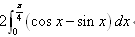 |
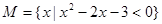 ,
,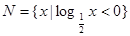 ,则
,则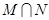 等于( )
等于( )A.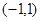 | B.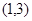 | C.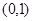 | D.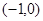 |
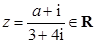 ,则实数
,则实数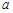 的值是( ).
的值是( ).A.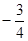 | B.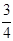 | C.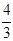 | D.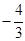 |
A.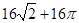 | B.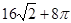 | C.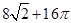 | D.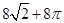 |
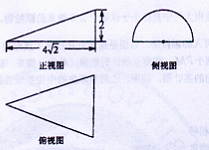
 满足约束条件
满足约束条件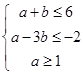 ,
, ,则
,则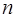 取最小值时,
取最小值时,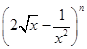 二项展开式中的常数项为 ( )
二项展开式中的常数项为 ( )A.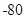 | B.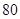 | C.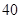 | D.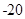 |
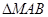 是直角三角形,则此双曲线的离心率e的值为 ( )
是直角三角形,则此双曲线的离心率e的值为 ( )A.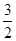 | B.2 | C.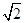 | D.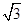 |
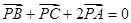 ,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )A.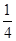 | B.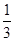 | C.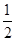 | D. |
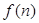 ,则
,则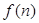 的递推关系式为 .
的递推关系式为 .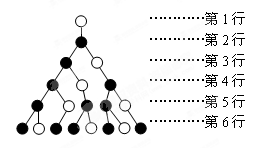
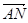 =
=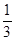
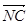 ,P是BN上的一点,若
,P是BN上的一点,若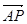 =m
=m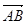 +
+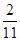
 ,则实数
,则实数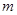 的值为___________.
的值为___________.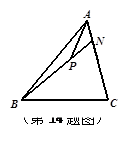
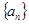 前9项的和等于前4项的和.若
前9项的和等于前4项的和.若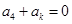 ,则k =________.
,则k =________.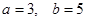 时,输出的值
时,输出的值 .
.
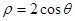 ,则曲线C上的点到直线
,则曲线C上的点到直线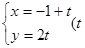 为参数)的距离的最小值为 .
为参数)的距离的最小值为 .
 )°C,培养时间在16小时以上,某制药厂为了缩短时间,决定优选培养温度,试验范围固定在
)°C,培养时间在16小时以上,某制药厂为了缩短时间,决定优选培养温度,试验范围固定在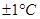 ,用分数法安排实验,令第一试点在
,用分数法安排实验,令第一试点在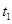 处,第二试点在
处,第二试点在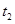 处,则
处,则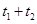 = 。
= 。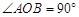 ,
,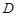 为
为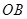 的中点,
的中点,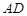 的延长线交⊙O于点
的延长线交⊙O于点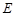 ,则线段
,则线段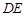 的长为
的长为 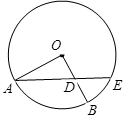
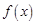 的定义域为
的定义域为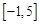 ,部分对应值如下表.
,部分对应值如下表.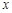 | -1 | 0 | 4 | 5 |
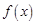 | 1 | 2 | 2 | 1 |
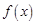 的导函数
的导函数 的图象如图所示:
的图象如图所示:
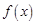 的命题:
的命题: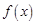 是周期函数;②函数
是周期函数;②函数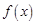 在
在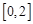 是减函数;
是减函数;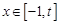 时,
时,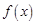 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;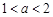 时,函数
时,函数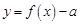 有4个零点;
有4个零点;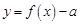 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个. ,函数
,函数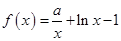 (其中
(其中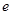 为自然对数的底数).
为自然对数的底数).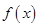 在区间
在区间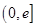 上的最小值;
上的最小值;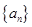 的通项
的通项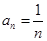 ,
,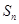 是前
是前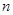 项和,证明:
项和,证明: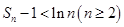 .
.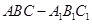 中,
中,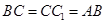 ="2" ,
="2" ,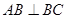 .点
.点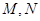 分别是
分别是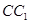 ,
,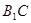 的中点,
的中点,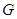 是棱
是棱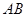 上的动点.
上的动点.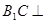 平面
平面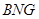 ;
;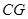 //平面
//平面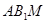 ,试确定
,试确定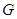 点的位置,
点的位置,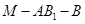 的余弦值.
的余弦值. 【
【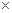 0.785,汽车的碳排放量(千克)=油耗公升数
0.785,汽车的碳排放量(千克)=油耗公升数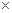 0.785等。怀化某中学高一一同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例P数据如右:
0.785等。怀化某中学高一一同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例P数据如右:
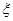 表示25个人中低碳族人数,求E
表示25个人中低碳族人数,求E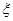 .
.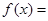
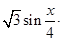
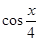
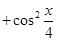 .
.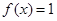 ,求
,求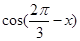 的值;
的值;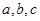 ,且满足
,且满足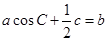 ,求
,求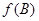 的取值范围.
的取值范围.
 到定点
到定点 的距离比到
的距离比到 轴的距离大
轴的距离大 .记点
.记点 的轨迹为曲线C.
的轨迹为曲线C. 的轨迹方程;
的轨迹方程; ,且圆心M在P的轨迹上,
,且圆心M在P的轨迹上, 是圆M在
是圆M在 轴的截得的弦,当M运动时弦长
轴的截得的弦,当M运动时弦长 是否为定值?说明理由;
是否为定值?说明理由; 作互相垂直的两直线交曲线C于G、H、R、S,求四边形面
作互相垂直的两直线交曲线C于G、H、R、S,求四边形面 的最小值.
的最小值.