适用年级:{{getGradeNameByProperty('高三|高考模拟|北京|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|高考模拟|北京|2014年')}} 使用省份:{{getAreaName('高三|高考模拟|北京|2014年')}}
试卷年份:{{getYear('高三|高考模拟|北京|2014年')}}上传日期:2014-05-21题数:20
提示:单击题文可显示答案与解析。
题号:918898
题型:选择题
难易度:较难
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
题号:918899
题型:选择题
难易度:一般
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天的回报比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报是前一天的两倍.
若投资的时间为
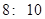
天,为使投资的回报最多,你会选择哪种方案投资?( )
题号:918900
题型:选择题
难易度:较易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】下列函数中,对于任意的
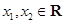
,满足条件
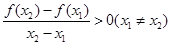
的函数是( )
题号:918901
题型:选择题
难易度:较易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】某几何体的三视图如图所示,则该几何体的体积是( )
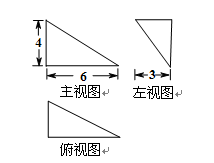
题号:918902
题型:选择题
难易度:较易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】已知命题
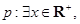
使得
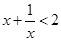
;命题
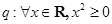
.则下列命题为真命题的是( )
题号:918903
题型:选择题
难易度:较易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
题号:918904
题型:选择题
难易度:较易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
题号:918905
题型:选择题
难易度:容易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】 在复平面内,复数
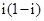
对应的点位于( )
题号:918893
题型:填空题
难易度:较难
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】在边长为2的菱形
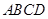
中,
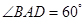
,若
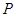
为
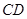
的中点,则
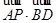
的值为____;若点
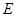
为
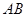
边上的动点,点
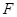
是
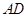
边上的动点,且
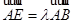
,
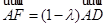
,
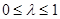
,则
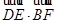
的最大值为________ .
题号:918894
题型:填空题
难易度:一般
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】已知矩形
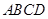
中,
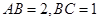
,在矩形
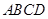
内随机取一点
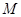
,则
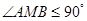
的概率为__________ .
题号:918895
题型:填空题
难易度:较易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】 已知双曲线
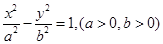
的焦距为
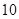
,一条渐近线的斜率为
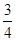
,则此双曲线的标准方程为______,焦点到渐近线的距离为_____ .
题号:918896
题型:填空题
难易度:一般
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
题号:918897
题型:填空题
难易度:较易
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
题号:3496422
题型:填空题
难易度:一般
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
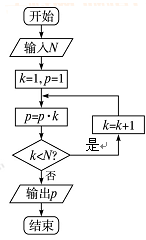
【题文】 执行右边的程序框图,若输入的N是4,则输出p的值是______ .
题号:918867
题型:解答题
难易度:较难
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】已知椭圆
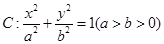
的焦点为
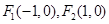
,点
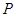
是椭圆
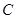
上的一点,
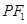
与
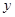
轴的交点
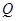
恰为
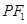
的中点,
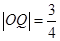
.
(1)求椭圆
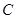
的方程;
(2)若点
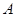
为椭圆的右顶点,过焦点
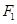
的直线与椭圆
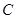
交于不同的两点
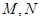
,求
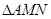
面积的取值范围.
题号:918868
题型:解答题
难易度:较难
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】已知函数
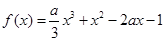
,
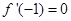
.
(1)求函数
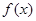
的单调区间;
(2)如果对于任意的
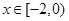
,都有
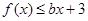
,求
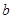
的取值范围.
题号:918869
题型:解答题
难易度:一般
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】已知等差数列
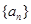
的前
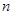
项和为
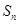
,公差
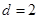
,且
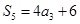
.
(1)求数列
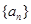
的通项公式;
(2)设数列
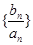
是首项为1,公比为
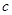
的等比数列,求数列
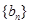
的前n项和
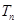
.
题号:918870
题型:解答题
难易度:较难
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】已知正四棱柱
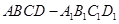
中,
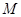
是
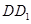
的中点.
(1)求证:
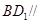
平面
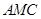
;
(2)求证:
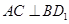
;
(3)在线段
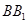
上是否存在点
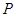
,当
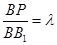
时,平面
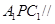
平面
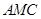
?若存在,求出
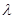
的值并证明;若不存在,请说明理由.
题号:918871
题型:解答题
难易度:一般
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】某学校为调查高一新生上学路程所需要的时间(单位:分钟),从高一年级新生中随机抽取100名新生按上学所需时间分组:第1组
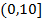
,第2组
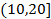
,第3组
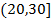
,第4组
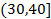
,第5组
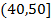
,得到的频率分布直方图如图所示.
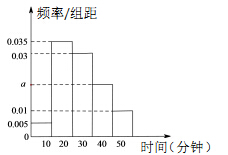
(1)根据图中数据求
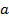
的值;
(2)若从第3,4,5组中用分层抽样的方法抽取6名新生参与交通安全问卷调查,应从第3,4,5组各抽取多少名新生?
(3)在(2)条件下,该校决定从这6名新生中随机抽取2名新生参加交通安全宣传活动,求第4组至少有一名志愿者被抽中的概率.
题号:918892
题型:解答题
难易度:一般
日期:2014-05-21
来源:2014届北京市昌平区高三第二次统练文科数学试卷(带解析)
【题文】已知函数
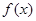
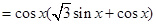
,
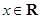
.
(1)求
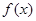
的最小正周期及值域;
(2)求
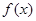
单调递增区间.
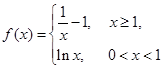 ,若
,若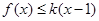 恒成立,则
恒成立,则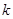 的取值范围是( )
的取值范围是( )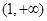
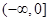
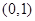
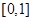
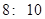 天,为使投资的回报最多,你会选择哪种方案投资?( )
天,为使投资的回报最多,你会选择哪种方案投资?( )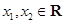 ,满足条件
,满足条件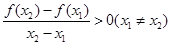 的函数是( )
的函数是( )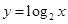
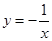
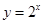
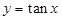

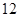
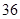
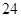
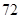
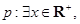 使得
使得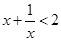 ;命题
;命题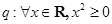 .则下列命题为真命题的是( )
.则下列命题为真命题的是( )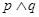
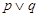
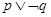
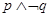
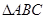 中,若
中,若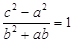 ,则
,则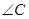 的大小为( )
的大小为( )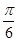
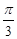
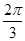
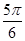
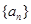 中,
中,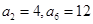 ,则
,则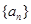 的前10项和为( )
的前10项和为( )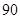
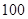
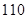
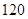
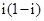 对应的点位于( )
对应的点位于( )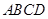 中,
中,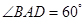 ,若
,若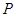 为
为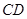 的中点,则
的中点,则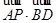 的值为____;若点
的值为____;若点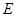 为
为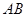 边上的动点,点
边上的动点,点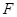 是
是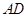 边上的动点,且
边上的动点,且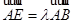 ,
,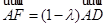 ,
, 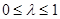 ,则
,则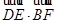 的最大值为________ .
的最大值为________ .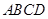 中,
中,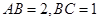 ,在矩形
,在矩形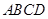 内随机取一点
内随机取一点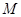 ,则
,则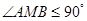 的概率为__________ .
的概率为__________ .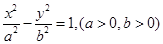 的焦距为
的焦距为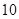 ,一条渐近线的斜率为
,一条渐近线的斜率为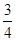 ,则此双曲线的标准方程为______,焦点到渐近线的距离为_____ .
,则此双曲线的标准方程为______,焦点到渐近线的距离为_____ .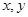 满足
满足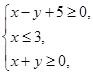 则
则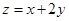 的最小值为_____ .
的最小值为_____ .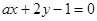 与直线
与直线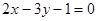 平行,则
平行,则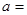 ______ .
______ .
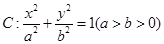 的焦点为
的焦点为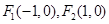 ,点
,点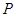 是椭圆
是椭圆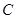 上的一点,
上的一点,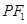 与
与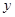 轴的交点
轴的交点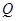 恰为
恰为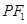 的中点,
的中点,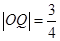 .
.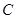 的方程;
的方程;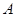 为椭圆的右顶点,过焦点
为椭圆的右顶点,过焦点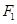 的直线与椭圆
的直线与椭圆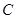 交于不同的两点
交于不同的两点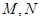 ,求
,求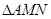 面积的取值范围.
面积的取值范围.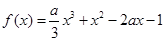 ,
,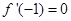 .
.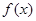 的单调区间;
的单调区间;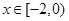 ,都有
,都有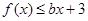 ,求
,求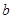 的取值范围.
的取值范围.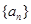 的前
的前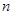 项和为
项和为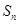 ,公差
,公差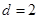 ,且
,且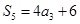 .
.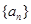 的通项公式;
的通项公式;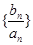 是首项为1,公比为
是首项为1,公比为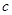 的等比数列,求数列
的等比数列,求数列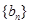 的前n项和
的前n项和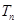 .
.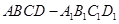 中,
中,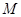 是
是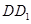 的中点.
的中点. 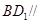 平面
平面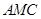 ;
;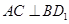 ;
;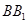 上是否存在点
上是否存在点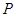 ,当
,当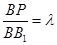 时,平面
时,平面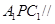 平面
平面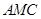 ?若存在,求出
?若存在,求出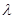 的值并证明;若不存在,请说明理由.
的值并证明;若不存在,请说明理由.
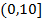 ,第2组
,第2组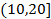 ,第3组
,第3组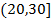 ,第4组
,第4组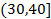 ,第5组
,第5组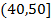 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
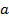 的值;
的值;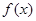
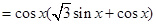 ,
,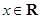 .
.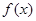 的最小正周期及值域;
的最小正周期及值域;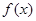 单调递增区间.
单调递增区间.