适用年级:{{getGradeNameByProperty('高三|高考真卷|北京|2011年')}} 试卷类型:{{getTestPaperTypeName('高三|高考真卷|北京|2011年')}} 使用省份:{{getAreaName('高三|高考真卷|北京|2011年')}}
试卷年份:{{getYear('高三|高考真卷|北京|2011年')}}上传日期:2011-06-30题数:19
提示:单击题文可显示答案与解析。
题号:1142721
题型:选择题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】若
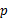
是真命题,

是假命题,则()
题号:1142722
题型:选择题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】如果

,那么
题号:1142723
题型:选择题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】复数

()
题号:1142724
题型:选择题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】已知全集U=R,集合

,那么
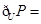
题号:3766541
题型:选择题
难易度:一般
日期:2012-09-06
来源:2011年普通高中招生考试北京市高考文科数学
题号:3766542
题型:选择题
难易度:一般
日期:2012-04-23
来源:2011年普通高中招生考试北京市高考文科数学
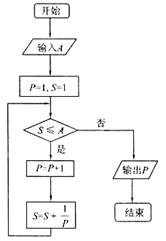
【题文】执行如图所示的程序框图,若输入A的值为2,则输出的P值为
题号:3766543
题型:选择题
难易度:一般
日期:2012-07-20
来源:2011年普通高中招生考试北京市高考文科数学
【题文】某车间分批生产某种产品,每批的生产准备费用为800元。若每批生产
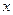
件,则平均仓储时间为

天,且每件产品每天的仓储费用为1元。为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品
题号:3766544
题型:选择题
难易度:一般
日期:2013-02-23
来源:2011年普通高中招生考试北京市高考文科数学
【题文】已知点
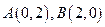
。若点

在函数

的图象上,则使得

的面积为2的点

的个数为
题号:1142716
题型:填空题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】设
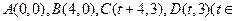
R)。记

为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则

;

的所有可能取值为
。
题号:1142717
题型:填空题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
题号:1142718
题型:填空题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
题号:1142719
题型:填空题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
题号:1142720
题型:填空题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
题号:3766547
题型:填空题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】已知函数若关于
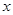
的方程

有两个不同的实根,则实数

的取值范围是
.
题号:1142712
题型:解答题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】本小题共13分)
若数列
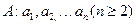
满足
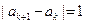
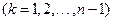
,则称
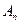
为
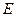
数列。记

。
(Ⅰ)写出一个
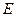
数列
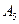
满足
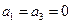
;
(Ⅱ)若

,证明:
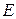
数列
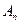
是递增数列的充要条件是

;
(Ⅲ)在
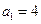
的
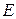
数列
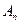
中,求使得
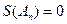
成立的
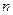
的最小值。
题号:1142713
题型:解答题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】(本小题共13分)
已知函数

。
(Ⅰ)求

的单调区间;
(Ⅱ)求

在区间
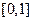
上的最小值。
题号:1142714
题型:解答题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】(本小题共14分)

如图,在四面体

中,
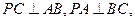
点
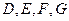
分别是棱
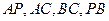
的中点。
(Ⅰ)求证:
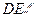
平面
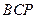
;
(Ⅱ)求证:四边形

为矩形;
(Ⅲ)是否存在点
,到四面体

六条棱的中点 的距离相等?说明理由。
题号:3766545
题型:解答题
难易度:一般
日期:2013-05-02
来源:2011年普通高中招生考试北京市高考文科数学
【题文】(本小题共13分)
以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经
X表示。

(Ⅰ)如果
X=8,求乙组同学植树棵数的平均数和方差;
(Ⅱ)如果
X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率。
(注:方差
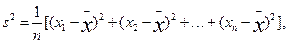
其中
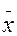
为
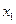
,

,

的平均数)
题号:3766546
题型:解答题
难易度:一般
日期:2011-06-30
来源:2011年普通高中招生考试北京市高考文科数学
【题文】已知椭圆

的离心率为

,右焦点为
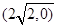
。斜率为1的直线

与椭圆
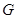
交于
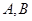
两点,以

为底边作等腰三角形,顶点为

。
(1)求椭圆
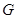
的方程;
(2)求
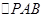
的面积。
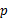 是真命题,
是真命题, 是假命题,则()
是假命题,则() 是真命题
是真命题 是假命题
是假命题 是真命题
是真命题 是真命题
是真命题 ,那么
,那么
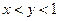
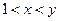

 ()
()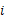
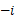
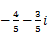
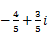
 ,那么
,那么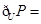
 )
)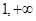 )
)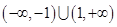




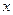 件,则平均仓储时间为
件,则平均仓储时间为 天,且每件产品每天的仓储费用为1元。为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品
天,且每件产品每天的仓储费用为1元。为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品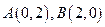 。若点
。若点 在函数
在函数 的图象上,则使得
的图象上,则使得 的面积为2的点
的面积为2的点 的个数为
的个数为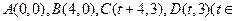 R)。记
R)。记 为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则
为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则 ;
; 的所有可能取值为 。
的所有可能取值为 。  中,若
中,若 则公比
则公比 ;
;
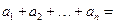 .
. 。若
。若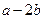 与
与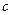 ,共线,则
,共线,则 = .
= . 的一条渐近线的方程为
的一条渐近线的方程为 ,则
,则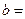 .
. 中,若
中,若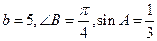 ,则
,则 .
.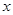 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是 .
的取值范围是 . 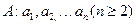 满足
满足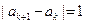
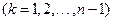 ,则称
,则称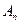 为
为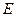 数列。记
数列。记 。
。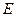 数列
数列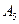 满足
满足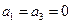 ;
; ,证明:
,证明: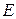 数列
数列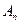 是递增数列的充要条件是
是递增数列的充要条件是 ;
;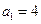 的
的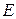 数列
数列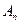 中,求使得
中,求使得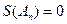 成立的
成立的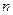 的最小值。
的最小值。 。
。 的单调区间;
的单调区间; 在区间
在区间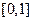 上的最小值。
上的最小值。
 中,
中,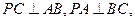 点
点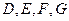 分别是棱
分别是棱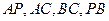 的中点。
的中点。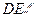 平面
平面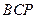 ;
; 为矩形;
为矩形;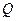 ,到四面体
,到四面体 六条棱的中点 的距离相等?说明理由。
六条棱的中点 的距离相等?说明理由。
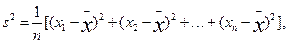 其中
其中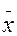 为
为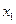 ,
, ,
,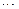
 的平均数)
的平均数)  的离心率为
的离心率为 ,右焦点为
,右焦点为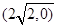 。斜率为1的直线
。斜率为1的直线 与椭圆
与椭圆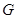 交于
交于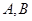 两点,以
两点,以 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为 。
。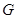 的方程;
的方程;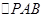 的面积。
的面积。